Условие задачи:
Определить напряженность электрического поля в точке, находящейся на расстоянии 20 см от поверхности заряженной проводящей сферы радиусом 10 см, если потенциал сферы равен 240 В.
Задача №6.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=20\) см, \(R=10\) см, \(\varphi=240\) В, \(E-?\)
Решение задачи:
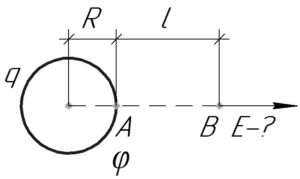 Потенциал сферы \(\varphi\) (т.е. потенциал в точке A — смотрите схему) радиусом \(R\), несущей некоторый заряд \(q\), можно определить так:
Потенциал сферы \(\varphi\) (т.е. потенциал в точке A — смотрите схему) радиусом \(R\), несущей некоторый заряд \(q\), можно определить так:
\[\varphi = \frac{{kq}}{R}\;\;\;\;(1)\]
Модуль напряженности электрического поля \(E\), создаваемого заряженной сферой с зарядом \(q\) и радиусом \(R\), на расстоянии \(l\) от поверхности сферы (в точке B — смотрите схему) легко найти по формуле:
\[E = \frac{{kq}}{{{{\left( {R + l} \right)}^2}}}\;\;\;\;(2)\]
Поделим (2) на (1), тогда:
\[\frac{E}{\varphi } = \frac{R}{{{{\left( {R + l} \right)}^2}}}\]
В итоге получим:
\[E = \frac{{\varphi R}}{{{{\left( {R + l} \right)}^2}}}\]
Численно напряженность электрического поля \(E\) равна:
\[E = \frac{{240 \cdot 0,1}}{{{{\left( {0,1 + 0,2} \right)}^2}}} = 266,7\;В/м \approx 2,67\;В/см\]
Ответ: 2,67 В/см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.3 При сообщении металлической сфере радиусом 10 см некоторого заряда
6.3.5 На расстоянии 10 м от центра заряженного металлического шара радиусом 3 м
6.3.6 Определить потенциал шара радиусом 10 см, находящегося в вакууме

 icodepro.ru
icodepro.ru