Условие задачи:
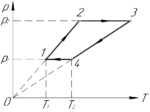 Определите работу, совершаемую одним молем газа за цикл, если \(\frac{p_2}{p_1}=2\), \(T_1=280\) К, \(T_2=360\) К (схема к условию приведена справа).
Определите работу, совершаемую одним молем газа за цикл, если \(\frac{p_2}{p_1}=2\), \(T_1=280\) К, \(T_2=360\) К (схема к условию приведена справа).
Задача №5.4.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=1\) моль, \(\frac{p_2}{p_1}=2\), \(T_1=280\) К, \(T_2=360\) К, \(A-?\)
Решение задачи:
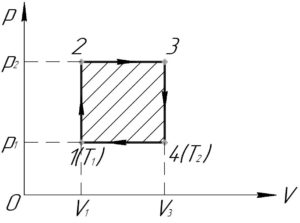 Приведённый в условии график для нахождения работы газа в цикле \(A\) перестроим в координатах p-V. Для этого нужно произвести анализ каждого из процессов.
Приведённый в условии график для нахождения работы газа в цикле \(A\) перестроим в координатах p-V. Для этого нужно произвести анализ каждого из процессов.
Итак, начнём. Процесс 1-2 — изохорный (\(V=const\)), поскольку график этого процесса в координатах p-T лежит на прямой, проходящей через начало координат. Так как температура газа в процессе увеличивается, то по закону Шарля давление растёт (хотя это итак понятно из исходного графика). Аналогично, изохорным является процесс 3-4, но так как температура газа в этом процессе уменьшается, то будет уменьшаться и давление.
Процесс 2-3 — изобарный (\(p=const\)). Температура газа в процессе растёт, поэтому по закону Гей-Люссака будет увеличиваться и объем. Также изобарным является процесс 4-1. Объем газа в этом процессе уменьшается, так как уменьшается температура.
С учётом всего вышесказанного получим следующий график (смотрите схему к решению).
Работа газа в цикле \(A\) равна площади этого цикла в координатах p-V. Если цикл обходится по часовой стрелке, то работа положительна (что имеет место в нашем случае), иначе — отрицательна. Тогда:
\[A = \left( {{p_2} — {p_1}} \right)\left( {{V_3} — {V_1}} \right)\;\;\;\;(1)\]
Запишем закон Гей-Люссака для изобарного процесса 4-1:
\[\frac{{{V_3}}}{{{T_2}}} = \frac{{{V_1}}}{{{T_1}}}\]
\[{V_3} = {V_1}\frac{{{T_2}}}{{{T_1}}}\;\;\;\;(2)\]
Учитывая выражение (2) и то, что по условию \(\frac{p_2}{p_1}=2\), формула (1) примет вид:
\[A = \left( {2{p_1} — {p_1}} \right)\left( {{V_1}\frac{{{T_2}}}{{{T_1}}} — {V_1}} \right) = {p_1}{V_1}\left( {\frac{{{T_2}}}{{{T_1}}} — 1} \right)\]
Теперь запишем уравнение Клапейрона-Менделеева для состояния газа в точке 1:
\[{p_1}{V_1} = \nu R{T_1}\]
Тогда:
\[A = \nu R{T_1}\left( {\frac{{{T_2}}}{{{T_1}}} — 1} \right)\]
\[A = \nu R\left( {{T_2} — {T_1}} \right)\]
Посчитаем ответ:
\[A = 1 \cdot 8,31 \cdot \left( {360 — 280} \right) = 664,8\;Дж\]
Ответ: 664,8 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.4.33 Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают
5.4.35 В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К
5.4.36 Два одинаковых сосуда, содержащих одинаковое число молекул азота, соединены

 icodepro.ru
icodepro.ru
почему на V2 поставили V3
Не так важно, но лучше конечно же писать V2