Решение: Луч белого света падает на поверхность воды под углом 60°. Чему равен угол

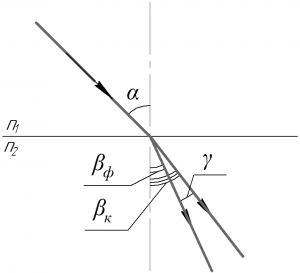
Условие задачи:

Луч белого света падает на поверхность воды под углом 60°. Чему равен угол \(\gamma\) между направлениями крайних красных и крайних фиолетовых лучей в воде, если показатели преломления их равны соответственно 1,329 и 1,344?

Задача №10.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=60^\circ\), \(n_{к2}=1,329\), \(n_{ф2}=1,344\), \(\gamma-?\)

Решение задачи:

Из рисунка к задаче понятно, что искомый угол \(\gamma\) можно найти следующим образом:

\[\gamma = {\beta _к} – {\beta _ф}\;\;\;\;(1)\]

Запишем дважды закон преломления света (также известен как закон преломления Снеллиуса):

\[\left\{ \begin{gathered}
{n_1}\sin \alpha = {n_{к2}}\sin {\beta _к} \hfill \\
{n_1}\sin \alpha = {n_{ф2}}\sin {\beta _ф} \hfill \\
\end{gathered} \right.\]

Здесь \(\alpha\) – угол падения луча белого света, \(\beta_к\) и \(\beta_ф\) – угол преломления красного и фиолетового луча соответственно, \(n_1\), \(n_{к2}\) и \(n_{ф2}\) – показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды для лучей с различной длиной волны смотри условие задачи.

Тогда:

\[\left\{ \begin{gathered}
\frac{{{n_1}\sin \alpha }}{{{n_{к2}}}} = \sin {\beta _к} \hfill \\
\frac{{{n_1}\sin \alpha }}{{{n_{ф2}}}} = \sin {\beta _ф} \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
{\beta _к} = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_{к2}}}}} \right) \hfill \\
{\beta _ф} = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_{ф2}}}}} \right) \hfill \\
\end{gathered} \right.\]

Тогда формула (1) примет следующий вид:

\[\gamma = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_{к2}}}}} \right) – \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_{ф2}}}}} \right)\]

Задача решена в общем виде, посчитаем численный ответ:

\[\gamma = \arcsin \left( {\frac{{1 \cdot \sin 60^\circ }}{{1,329}}} \right) – \arcsin \left( {\frac{{1 \cdot \sin 60^\circ }}{{1,344}}} \right) = 0,55^\circ \]