Условие задачи:
На дифракционную решетку с периодом 4 мкм падает нормально монохроматическая волна. Определить длину волны, если первый максимум на экране в 40 см от решетки получается на расстоянии 5 см от центрального.
Задача №10.7.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=4\) мкм, \(k=1\), \(L=40\) см, \(l=5\) см, \(\lambda-?\)
Решение задачи:
 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
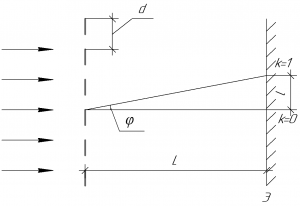
В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума (в данной задаче \(k=1\)), \(\lambda\) — длина волны, падающей нормально на решетку.
Если расписать синус угла дифракции (см. рисунок к задаче), то имеем:
\[d\frac{l}{{\sqrt {{L^2} + {l^2}} }} = k\lambda \]
Осталось из полученной формулы выразить искомую длину волны \(\lambda\):
\[\lambda = \frac{{dl}}{{k\sqrt {{L^2} + {l^2}} }}\]
Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:
\[\lambda = \frac{{4 \cdot {{10}^{ — 6}} \cdot 0,05}}{{1 \cdot \sqrt {{{0,4}^2} + {{0,05}^2}} }} = 0,5 \cdot {10^{ — 6}}\;м = 500\;нм\]
Ответ: 500 нм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.26 Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м
10.7.28 При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное
10.7.29 На каком расстоянии от дифракционной решетки надо поставить экран, чтобы расстояние

 icodepro.ru
icodepro.ru благодарю за решение
благодарю за решение