Решение: На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света

Условие задачи:

На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света. На поверхности воды плавает круглый диск, центр которого находится над источником. При каком минимальном радиусе диска лучи от источника не будут выходить из воды?

Задача №10.4.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=0,4\) м, \(r-?\)

Решение задачи:

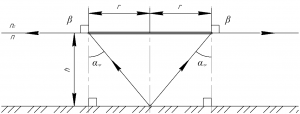Если лучи от источника, которые уже не попадают на диск, будут идти под углами большими, чем угол полного внутреннего отражения, то никакие лучи из воды выходить не будут (см. рисунок к задаче).

Из прямоугольного треугольника можно найти искомый радиус \(r\):

\[r = h \cdot tg{\alpha _{пр}}\;\;\;\;(1)\]

Запишем закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения при переходе светового луча из воды в воздух:

\[n\sin \alpha_{пр} = {n_0}\sin {\beta}\]

Здесь \(\alpha_{пр}\) — предельный угол полного внутреннего отражения, \(\beta\) — угол преломления, равный в данном случае 90°, \(n\) и \(n_0\) — показатели преломления сред. Показатель преломления воздуха \(n_0\) равен 1, показатель преломления воды \(n\) равен 1,33. Так как \(n_0=1\) и \(\sin \beta_0 = 1\), то:

\[n\sin {\alpha _{пр}} = 1\]

\[\sin {\alpha _{пр}} = \frac{1}{n}\]

\[{\alpha _{пр}} = \arcsin \left( {\frac{1}{n}} \right)\]

Осталось только полученное выражение подставить в формулу (1):

\[r = h \cdot tg\left( {\arcsin \left( {\frac{1}{n}} \right)} \right)\]

Задача решена, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[r = 0,4 \cdot tg\left( {\arcsin \left( {\frac{1}{{1,33}}} \right)} \right) = 0,456\;м = 45,6\;см\]