Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа

Условие задачи:

Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа. Максимальное расстояние, на которое может отойти человек ростом 1,8 м от края бассейна, чтобы видеть изображение лампы в воде, равно 3 м. На каком расстоянии от своих глаз наблюдатель видит изображение лампы?

Задача №10.1.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(r=5\) м, \(h=1,8\) м, \(l=3\) м, \(L-?\)

Решение задачи:

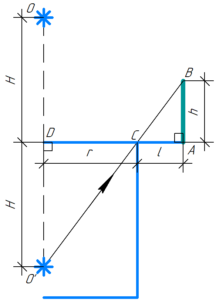Для решения задачи нужно сделать рисунок. Условно покажем человека AB ростом \(h\), стоящего на расстоянии \(l\) от края бассейна радиусом \(r\). Через голову человека B и край бассейна C проведем некоторый луч – это крайнее направление лучей, при котором человек ещё видит изображение лампы в воде. От центра бассейна проведем перпендикуляр до пересечения с лучом, в месте пересечения должно находится изображение лампы O’ в воде. Изображение лампы находится на некоторой глубине \(H\), сама же лампа O находится на такой же высоте над центром бассейна (правило построения изображения в воде такое же, как правило построения изображения в зеркале).

Из рисунка прекрасно видно, что искомое расстояние \(L\) это сумма длин отрезков BC и CO’, которые легко можно определить, воспользовавшись теоремой Пифагора. Поэтому:

\[L = \sqrt {{h^2} + {l^2}} + \sqrt {{H^2} + {r^2}} \;\;\;\;(1)\]

Неизвестную величину \(H\) можно определить благодаря подобию треугольников ABC и CDO’. Тогда:

\[\frac{H}{h} = \frac{r}{l}\]

\[H = h\frac{r}{l}\;\;\;\;(2)\]

Подставим полученное выражение (2) в формулу (1):

\[L = \sqrt {{h^2} + {l^2}} + \sqrt {{h^2}\frac{{{r^2}}}{{{l^2}}} + {r^2}} \]

Вынесем \(r^2\) из второго корня:

\[L = \sqrt {{h^2} + {l^2}} + r\sqrt {\frac{{{h^2}}}{{{l^2}}} + 1} \]

Приведем во втором корне под общий знаменатель:

\[L = \sqrt {{h^2} + {l^2}} + r\sqrt {\frac{{{h^2} + {l^2}}}{{{l^2}}}} \]

Вынесем \(l^2\) из знаменателя дроби во втором корне:

\[L = \sqrt {{h^2} + {l^2}} + \frac{r}{l}\sqrt {{h^2} + {l^2}} \]

\[L = \left( {\frac{r}{l} + 1} \right)\sqrt {{h^2} + {l^2}} \]

Численный ответ равен:

\[L = \left( {\frac{5}{3} + 1} \right)\sqrt {{{1,8}^2} + {3^2}} = 9,33\;м\]

Ответ: 9,33 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.1.5 Луч света падает на систему двух взаимно перпендикулярных зеркал. Угол падения
10.1.7 Высота Солнца над горизонтом 38°. Под каким углом к горизонту надо расположить
10.1.8 Солнечный луч, проходящий через отверстие в ставне, составляет с поверхностью стола