Условие задачи:
Определить угол отклонения лучей монохроматического света с длиной волны 0,55 мкм в спектре первого порядка, полученном с помощью дифракционной решетки, период которой 0,02 мм.
Задача №10.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\lambda=0,55\) мкм, \(k=1\), \(d=0,02\) мм, \(\varphi-?\)
Решение задачи:
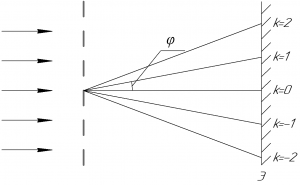 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума (по условию задачи — первый максимум), \(\lambda\) — длина волны, падающей нормально на решетку.
Из формулы (1) выразим искомый угол дифракции для максимума первого порядка (\(k=1\) по условию):
\[\sin \varphi = \frac{{k\lambda }}{d}\]
\[\varphi = \arcsin \left( {\frac{{k\lambda }}{d}} \right)\]
Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:
\[\varphi = \arcsin \left( {\frac{{1 \cdot 0,55 \cdot {{10}^{ — 6}}}}{{0,02 \cdot {{10}^{ — 3}}}}} \right) = 1,58^\circ \]
Ответ: 1,58°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.6.6 Тонкая мыльная пленка освещается светом с длиной волны 0,6 мкм. Чему равна
10.7.2 Один миллиметр дифракционной решетки содержит 20 штрихов. На какой угол отклоняются
10.7.3 Дифракционная решетка имеет 250 штрихов на миллиметр. Под каким углом виден максимум

 icodepro.ru
icodepro.ru