Решение: Под каким углом к поверхности стола надо расположить плоское зеркало, чтобы получить

Условие задачи:

Под каким углом к поверхности стола надо расположить плоское зеркало, чтобы получить изображение предмета, лежащего на столе, в вертикальной плоскости?

Задача №10.1.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=90^\circ\), \(\beta-?\)

Решение задачи:

Итак, для решения задачи, как и всегда в оптике, нужно сделать рисунок.

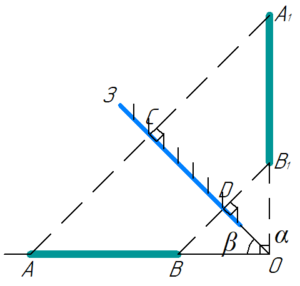
Изобразим предмет AB, лежащий на полу. Из условия задачи известно, что изображение предмета A₁B₁ в зеркале находится в вертикальной плоскости. Выберем некоторую произвольную точку O в плоскости пола, о назначении которой расскажем чуть позже. Изобразим вертикальное изображение предмета A₁B₁ так, что OA=OA₁ и OB=OB₁.

Точка O – это проекция на плоскость рисунка прямой, образованной при пересечении плоскости зеркала и плоскости пола. Указанные нами два условия (OA=OA₁ и OB=OB₁) – это математическое выражение того факта, что зеркало не искажает геометрические размеры.

Далее соединяем точку A с A₁ и B с B₁. Так как же изображение предмета в зеркале симметрично самому предмету относительно зеркала, то зеркало проходит через середины отрезков AA₁ и BB₁, то есть через точки C и D.

Треугольники AOC и A₁OC равны друг другу (по двум сторонам и углу между ними), поэтому углы AOC и A₁OC равны друг другу. Значит:

\[\alpha = \beta + \beta \]

\[\alpha = 2\beta \]

\[\beta = \frac{\alpha }{2}\]

Численный ответ равен:

\[\beta = \frac{{90^\circ }}{2} = 45^\circ \]