Условие задачи:
При нормальном падении белого света на дифракционную решетку зеленая линия (\(\lambda = 500\) нм) в спектре второго порядка видна под углом дифракции 30°. Найти число штрихов 1 мм длины этой решетки.
Задача №10.7.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\lambda=500\) нм, \(k=2\), \(\varphi=30^\circ\), \(l=1\) мм, \(N-?\)
Решение задачи:
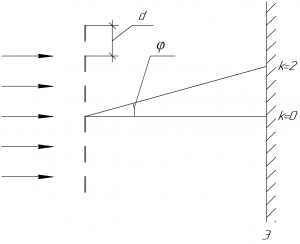 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума (по условию задачи — \(k=2\)), \(\lambda\) — длина волны, падающей нормально на решетку.
Период (постоянную) решетки \(d\) можно определить, разделив некоторую длину решетки \(l\) (в данном случае — 1 мм) на количество содержащихся на этой длине штрихов \(N\), то есть:
\[d = \frac{l}{N}\;\;\;\;(2)\]
Подставим (2) в (1), тогда будем иметь:
\[\frac{l}{N}\sin \varphi = k\lambda \]
Из полученной формулы выразим искомое количество штрихов:
\[N = \frac{{l\sin \varphi }}{{k\lambda }}\]
Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:
\[N = \frac{{{{10}^{ — 3}} \cdot \sin {30^\circ }}}{{2 \cdot 500 \cdot {{10}^{ — 9}}}} = 500\]
Ответ: 500.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.36 На дифракционную решетку нормально падает пучок света от разрядной трубки
10.1.1 На какой угол повернется отраженный от зеркала солнечный луч при повороте зеркала
10.1.2 Предмет находился на расстоянии 20 см от плоского зеркала. Затем его отодвинули на 10 см

 icodepro.ru
icodepro.ru