Условие задачи:
Точечный предмет движется по окружности со скоростью 0,04 м/с вокруг главной оптической оси двояковыпуклой тонкой линзы в плоскости, перпендикулярной оси и отстоящей от линзы на расстоянии в 1,2 раза больше фокусного расстояния линзы. С какой скоростью движется изображение предмета?
Задача №10.5.72 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=0,04\) м/с, \(d=1,2F\), \(u-?\)
Решение задачи:
 Начнем с того, что двояковыпуклая тонкая линза в воздухе является собирающей линзой. Также отметим, что поперечные скорости предмета и изображения соотносятся между собой также, как и поперечные размеры предмета и изображения, то есть справедлива формула:
Начнем с того, что двояковыпуклая тонкая линза в воздухе является собирающей линзой. Также отметим, что поперечные скорости предмета и изображения соотносятся между собой также, как и поперечные размеры предмета и изображения, то есть справедлива формула:
\[u = \Gamma \upsilon \;\;\;\;(1)\]
Запишем формулу тонкой линзы:
\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\;\;\;\;(2)\]
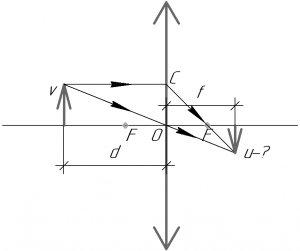
В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).
Из подобия изображенных на рисунке треугольников по трем углам следует, что (при этом эти две дроби ещё равны и поперечному увеличению линзы \(\Gamma\)):
\[\Gamma = \frac{f}{d} = \frac{h}{H}\]
\[\Gamma = \frac{f}{d}\;\;\;\;(3)\]
Тогда из формулы (2) выразим неизвестное расстояние от линзы до изображения \(f\):
\[\frac{1}{f} = \frac{1}{F} — \frac{1}{d}\]
\[\frac{1}{f} = \frac{{d — F}}{{dF}}\]
\[f = \frac{{dF}}{{d — F}}\;\;\;\;(4)\]
Подставим выражение (4) в формулу (3):
\[\Gamma = \frac{{dF}}{{d\left( {d — F} \right)}}\]
\[\Gamma = \frac{F}{{d — F}}\]
Полученное выражение подставим в формулу (1):
\[u = \frac{{F\upsilon }}{{d — F}}\]
По условию задачи \(d=1,2F\), поэтому:
\[u = \frac{{F\upsilon }}{{1,2F — F}}\]
\[u = 5\upsilon \]
Если подставить в полученную формулу численные значения величин из условия задачи, то мы получим ответ:
\[u = 5 \cdot 0,04 = 0,2\;м/с = 20\;см/с\]
Ответ: 20 см/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.71 Небольшому шарику, который находится на поверхности горизонтально расположенной
10.5.73 Укажите номер рисунка, на котором правильно изображен ход светового луча
10.6.1 Разность хода двух волн, полученных от когерентных источников до данной точки равна

 icodepro.ru
icodepro.ru