Условие задачи:
Два вольтметра, подключенные последовательно к ненагруженной батарее, показывают соответственно \(U_{11}=5\) В и \(U_{12}=15\) В. Если подключить к батарее только первый вольтметр, он покажет 19 В. Определить ЭДС батареи.
Задача №7.5.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U_{11}=5\) В, \(U_{12}=15\) В, \(U_2=19\) В, \(\rm E-?\)
Решение задачи:
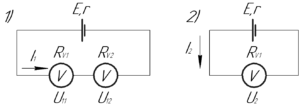 В задаче рассмотрено два случая, схемы для которых приведены на рисунке. Очевидно, что в первом случае напряжение во внешней цепи равно сумме напряжений \(U_{11}\) и \(U_{12}\), то есть:
В задаче рассмотрено два случая, схемы для которых приведены на рисунке. Очевидно, что в первом случае напряжение во внешней цепи равно сумме напряжений \(U_{11}\) и \(U_{12}\), то есть:
\[{U_1} = {U_{11}} + {U_{12}}\]
\[{U_1} = 5 + 15 = 20\;А\]
Должно быть понятно, что внутренние сопротивления вольтметров \(R_{v1}\) и \(R_{v2}\) различны, поскольку в противном случае напряжения \(U_{11}\) и \(U_{12}\) были бы равны. В первом случае через вольтметры, соединенные последовательно, течёт одинаковый ток, поэтому верно равенство:
\[\frac{{{U_{11}}}}{{{R_{v1}}}} = \frac{{{U_{12}}}}{{{R_{v2}}}}\]
Откуда имеем:
\[{R_{v2}} = {R_{v1}}\frac{{{U_{12}}}}{{{U_{11}}}}\]
Учитывая, что \(U_{11}=5\) В, а \(U_{12}=15\) В, получим:
\[{R_{v2}} = 3{R_{v2}}\]
Тогда в первом случае суммарное сопротивление двух вольтметров равно \(4R_{v1}\). Запишем закон Ома для полной цепи для двух случаев:
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{4{R_{v1}} + r}} \hfill \\
{I_2} = \frac{{\rm E}}{{{R_{v1}} + r}} \hfill \\
\end{gathered} \right.\]
Тогда напряжения во внешней цепи \(U_1\) и \(U_2\) в обоих случаях можно найти по формулам:
\[\left\{ \begin{gathered}
{U_1} = \frac{{{\rm E} \cdot 4{R_{v1}}}}{{4{R_{v1}} + r}} \;\;\;\;(1)\hfill \\
{U_2} = \frac{{{\rm E} \cdot {R_{v1}}}}{{{R_{v1}} + r}} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Разделим (1) на (2):
\[\frac{{{U_1}}}{{{U_2}}} = \frac{{4\left( {{R_{v1}} + r} \right)}}{{4{R_{v1}} + r}}\]
Учтем, что \(U_1=20\) В, а \(U_2=19\) В:
\[\frac{{20}}{{19}} = \frac{{4\left( {{R_{v1}} + r} \right)}}{{4{R_{v1}} + r}}\]
Перемножим «крест-накрест» и сразу же раскроем скобки:
\[80{R_{v1}} + 20r = 76{R_{v1}} + 76r\]
\[4{R_{v1}} = 56r\]
\[{R_{v1}} = 14r\]
Полученное выражение подставим в (2):
\[{U_2} = \frac{{{\rm E} \cdot 14r}}{{15r}}\]
\[{U_2} = \frac{{14{\rm E}}}{{15}}\]
Откуда окончательно получим:
\[{\rm E} = \frac{{15{U_2}}}{{14}}\]
Численный ответ равен:
\[{\rm E} = \frac{{15 \cdot 19}}{{14}} \approx 20,4\;В\]
Ответ: 20,4 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.27 К источнику тока подключены последовательно амперметр и резистор. Параллельно резистору
7.5.29 В цепь, состоящую из источника ЭДС и сопротивления 2 Ом, включают амперметр сначала
7.5.30 Каково удельное сопротивление проводника, если его длина 10 км, площадь поперечного

 icodepro.ru
icodepro.ru