Условие задачи:

Если подключить к гальванометру шунт 100 Ом, вся шкала соответствует току во внешней цепи 3 А. Если подключить к нему добавочное сопротивление 300 Ом шкала становится в 4 раза грубее. Какой шунт надо взять, чтобы стрелка отклонялась на всю шкалу при токе во внешней цепи 7,5 А?

Задача №7.5.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R_{ш1}=100\) Ом, \(I_1=3\) А, \(R_{доп}=300\) Ом, \(\frac{U_2}{U_0}=4\), \(I_3=7,5\) А, \(R_{ш3}-?\)

Решение задачи:

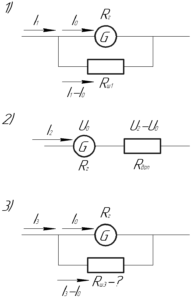Задачу будем решать с конца, проведем рассуждения для третьего случая (см. рисунок 3).

Величину сопротивления шунта \(R_{ш3}\) можно определить из следующих соображений. Так как амперметр и шунт соединены параллельно, то на них одинаковое напряжение \(U_3\). Сила тока на гальванометре не должна превышать предела измерения \(I_0\), тогда на шунте сила тока будет равна \(\left( {{I_3} — {I_0}} \right)\). Здесь \(I_3\) — сила тока на том участке, где нужно произвести измерение. Поэтому:

\[\left\{ \begin{gathered}
{U_3} = {I_0}{R_г} \hfill \\
{U_3} = \left( {{I_3} — {I_0}} \right){R_{ш3}} \hfill \\
\end{gathered} \right.\]

Тогда, очевидно, имеем:

\[{I_0}{R_г} = \left( {{I_3} — {I_0}} \right){R_{ш3}}\]

Получим такую формулу для нахождения искомого сопротивления шунта \(R_{ш3}\):

\[{R_{ш3}} = {R_г}\frac{{{I_0}}}{{{I_3} — {I_0}}}\;\;\;\;(1)\]

Чтобы определить предел измерения гальванометра \(I_0\), проведем аналогичные рассуждения для первого случая (см. рисунок 1) и получим такую систему:

\[\left\{ \begin{gathered}
{U_1} = {I_0}{R_г} \hfill \\
{U_1} = \left( {{I_1} — {I_0}} \right){R_{ш1}} \hfill \\
\end{gathered} \right.\]

Тогда:

\[{I_0}{R_г} = \left( {{I_1} — {I_0}} \right){R_{ш1}}\]

Раскроем скобки в правой части:

\[{I_0}{R_г} = {I_1}{R_{ш1}} — {I_0}{R_{ш1}}\]

\[{I_0}{R_г} + {I_0}{R_{ш1}} = {I_1}{R_{ш1}}\]

\[{I_0}\left( {{R_г} + {R_{ш1}}} \right) = {I_1}{R_{ш1}}\]

\[{I_0} = \frac{{{I_1}{R_{ш1}}}}{{{R_г} + {R_{ш1}}}}\;\;\;\;(2)\]

Теперь, чтобы определить сопротивление гальванометра \(R_г\), рассмотрим второй случай (см. рисунок 2). Здесь гальванометр используется как вольтметр. Так как гальванометр и добавочное сопротивление соединены последовательно, то через них течет одинаковый ток \(I_2\). Напряжение на гальванометре не должно превышать предела измерения (по напряжению) \(U_0\), тогда на добавочном сопротивлении напряжение будет равно \(\left( {{U_2} — {U_0}} \right)\). Запишем дважды закон Ома для участка цепи:

\[\left\{ \begin{gathered}
{I_2} = \frac{{{U_0}}}{{{R_г}}} \hfill \\
{I_2} = \frac{{{U_2} — {U_0}}}{{{R_{доп}}}} \hfill \\
\end{gathered} \right.\]

Тогда, очевидно, имеем:

\[\frac{{{U_0}}}{{{R_г}}} = \frac{{{U_2} — {U_0}}}{{{R_{доп}}}}\]

Откуда:

\[{R_г} = {R_{доп}}\frac{{{U_0}}}{{{U_2} — {U_0}}}\]

Разделим и числитель, и знаменатель в правой части на \(U_0\):

\[{R_г} = {R_{доп}}\frac{1}{{\frac{{{U_2}}}{{{U_0}}} — 1}}\]

По условию при подключении добавочного сопротивления шкала становится в 4 раза грубее, т.е. \(\frac{U_2}{U_0}=4\), поэтому:

\[{R_г} = \frac{{{R_{доп}}}}{3}\;\;\;\;(3)\]

Решать задачу в общем виде не будем, рассчитаем поочередно формулы (3), (2) и (1):

\[{R_г} = \frac{{300}}{3} = 100\;Ом\]

\[{I_0} = \frac{{3 \cdot 100}}{{100 + 100}} = 1,5\;А\]

\[{R_{ш2}} = 100 \cdot \frac{{1,5}}{{7,5 — 1,5}} = 25\;Ом\]

Ответ: 25 Ом.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.5.19 Вольтметр с внутренним сопротивлением 3 кОм, включенный в городскую осветительную сеть
7.5.21 Стрелка миллиамперметра отклоняется до конца шкалы, если через миллиамперметр идет ток
7.5.22 Гальванометр со шкалой из 50 делений имеет цену деления 2 мкА/дел

Встречают с улыбкой в чулках и на каблучках, лучшие феи проститутки Симферополь в красивом нижнем белье с feisimferopol.ru провожают поцелуем и ждут следующей встречи. Сегодня вполне реально заказать ночную фею на час или ночь по минимальной цене. Лучшие в городе лучшие феи проститутки Симферополь, страстные и желанные, они такие изобретательные и профессиональные, что любой захочет их. Не упусти свой шанс.