Решение: Гальванометр со шкалой из 50 делений имеет цену деления 2 мкА/дел

Условие задачи:

Гальванометр со шкалой из 50 делений имеет цену деления 2 мкА/дел и внутреннее сопротивление 200 Ом. Какое добавочное сопротивление следует подключить, чтобы его можно было использовать как вольтметр для измерения напряжения до 2 В?

Задача №7.5.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(N=50\), \(I_{дел}=2\) мкА, \(R_г=200\) Ом, \(U=2\) В, \(R_{доп}-?\)

Решение задачи:

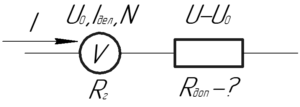Вы должны понимать, что если знать внутреннее сопротивление гальванометра (прибора, который измеряет токи малой силы), то им можно измерять также и напряжение (его можно вычислить по закону Ома). Поэтому не удивляйтесь, что дальнейшие рассуждения проведены как для вольтметра.

Если предел измерения гальванометра не позволяет измерить напряжение на этом участке, то к нему последовательно соединяют дополнительное (также называют добавочное) сопротивление \(R_{доп}\). Оно уменьшает значение напряжения на гальванометре.

При этом величину этого дополнительного сопротивления можно определить из следующих соображений. Так как гальванометр и добавочное сопротивление соединены последовательно, то через них течет одинаковый ток \(I\). Напряжение на гальванометре не должно превышать предела измерения, тогда на добавочном сопротивлении напряжение будет равно \(\left( {U – {U_0}} \right)\). Запишем дважды закон Ома для участка цепи:

\[\left\{ \begin{gathered}
I = \frac{{{U_0}}}{{{R_г}}} \hfill \\
I = \frac{{U – {U_0}}}{{{R_{доп}}}} \hfill \\
\end{gathered} \right.\]

Тогда, очевидно, имеем:

\[\frac{{{U_0}}}{{{R_г}}} = \frac{{U – {U_0}}}{{{R_{доп}}}}\]

Получим такую формулу:

\[{R_{доп}} = {R_г}\frac{{U – {U_0}}}{{{U_0}}}\]

Предел измерения гальванометра по напряжению \(U_0\) можно определить по такой формуле (закон Ома для участка цепи):

\[{U_0} = N{I_{дел}}{R_г}\]

Окончательно имеем:

\[{R_{доп}} = {R_г}\frac{{U – N{I_{дел}}{R_г}}}{{N{I_{дел}}{R_г}}}\]

\[{R_{доп}} = \frac{{U – N{I_{дел}}{R_г}}}{{N{I_{дел}}}}\]

Подставим численные данные задачи в эту формулу и посчитаем ответ:

\[{R_{доп}} = \frac{{2 – 50 \cdot 2 \cdot {{10}^{ – 6}} \cdot 200}}{{50 \cdot 2 \cdot {{10}^{ – 6}}}} = 19800\;Ом = 19,8\;кОм\]