Условие задачи:
Источник тока имеет ЭДС 12 В. Сила тока в цепи 4 А, напряжение на внешнем сопротивлении 11 В. Определите ток короткого замыкания.
Задача №7.2.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\rm E=12\) В, \(I=4\) А, \(U=11\) В, \(I_{кз}-?\)
Решение задачи:
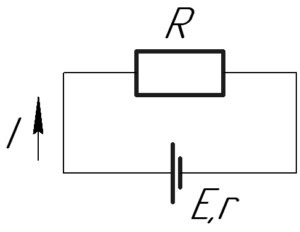 Ток короткого замыкания \(I_{кз}\) определяют по следующей формуле:
Ток короткого замыкания \(I_{кз}\) определяют по следующей формуле:
\[{I_{кз}} = \frac{{\rm E}}{r}\;\;\;\;(1)\]
Чтобы найти внутреннее сопротивление источника тока \(r\), запишем закон Ома для полной цепи:
\[I = \frac{{\rm E}}{{R + r}}\]
Откуда имеем:
\[R + r = \frac{{\rm E}}{I}\]
\[r = \frac{{\rm E}}{I} — R\;\;\;\;(2)\]
Чтобы найти внешнее сопротивление \(R\), запишем формулу для определения напряжения на внешнем сопротивлении (или на клеммах источника, это одно и то же):
\[U = IR\]
Откуда получим:
\[R = \frac{U}{I}\;\;\;\;(3)\]
Подставим (3) в (2):
\[r = \frac{{\rm E}}{I} — \frac{U}{I}\]
\[r = \frac{{{\rm E} — U}}{I}\]
Полученное подставим в (1):
\[{I_{кз}} = \frac{{{\rm E}I}}{{{\rm E} — U}}\]
Мы получили итоговую формулу, подставим числа в нее и посчитаем ответ:
\[{I_{кз}} = \frac{{12 \cdot 4}}{{12 — 11}} = 48\;А\]
Ответ: 48 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.29 Два источника с одинаковыми ЭДС 2 В и внутренними сопротивлениями 0,2 и 0,4 Ом соединены
7.2.31 Два элемента с внутренним сопротивлением 0,2 и 0,4 Ом соединены одинаковыми полюсами
7.2.32 Два элемента соединены параллельно. Один имеет ЭДС E1=2 В и внутреннее сопротивление

 icodepro.ru
icodepro.ru