Условие задачи:
Какова ЭДС источника, если при измерении напряжения на его зажимах вольтметром с внутренним сопротивлением 20 Ом мы получаем напряжение 1,37 В, а при замыкании источника на сопротивление 10 Ом получаем ток 0,132 А?
Задача №7.2.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_v=20\) Ом, \(U=1,37\) В, \(R=10\) Ом, \(I_2=0,132\) А, \(\rm E-?\)
Решение задачи:
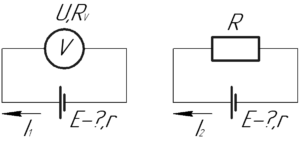 Напряжение, которое покажет вольтметр, можно рассчитать по такой формуле:
Напряжение, которое покажет вольтметр, можно рассчитать по такой формуле:
\[U = {I_1}{R_v}\;\;\;\;(1)\]
Ток \(I_1\), текущий через вольтметр, можно найти по закону Ома для полной цепи:
\[{I_1} = \frac{{\rm E}}{{{R_v} + r}}\]
Тогда формула (1) примет такой вид:
\[U = \frac{{{\rm E}{R_v}}}{{{R_v} + r}}\]
Выразим ЭДС:
\[{\rm E} = \frac{{U\left( {{R_v} + r} \right)}}{{{R_v}}}\;\;\;\;(2)\]
\[{\rm E} = U\left( {1 + \frac{r}{{{R_v}}}} \right)\;\;\;\;(3)\]
Ток \(I_2\), текущий через сопротивление \(R\), также определим по закону Ома для полной цепи:
\[{I_2} = \frac{{\rm E}}{{R + r}}\]
Откуда ЭДС:
\[{\rm E} = {I_2}\left( {R + r} \right)\;\;\;\;(4)\]
Приравняем (2) и (4), получим такое равенство:
\[U\frac{{{R_v} + r}}{{{R_v}}} = {I_2}\left( {R + r} \right)\]
\[U\left( {{R_v} + r} \right) = {I_2}{R_v}\left( {R + r} \right)\]
Раскроем скобки в обеих частях равенства, все члены с неизвестным \(r\) перенесем в правую часть, остальные — в левую, далее вынесем неизвестное внутреннее сопротивление \(r\) за скобки и выразим его:
\[U{R_v} + Ur = {I_2}{R_v}R + {I_2}{R_v}r\]
\[U{R_v} — {I_2}{R_v}R = {I_2}{R_v}r — Ur\]
\[r\left( {{I_2}{R_v} — U} \right) = {R_v}\left( {U — {I_2}R} \right)\]
\[r = \frac{{{R_v}\left( {U — {I_2}R} \right)}}{{{I_2}{R_v} — U}}\]
Отлично, мы выразили неизвестное внутреннее сопротивление \(r\) через известные величины, осталось только полученное выражение подставить в формулу (3), чтобы получить решение задачи в общем виде. Получим:
\[{\rm E} = U\left( {1 + \frac{{U — {I_2}R}}{{{I_2}{R_v} — U}}} \right)\]
Приведем в скобках под общий знаменатель:
\[{\rm E} = U\frac{{{I_2}{R_v} — U + U — {I_2}R}}{{{I_2}{R_v} — U}}\]
\[{\rm E} = U\frac{{{I_2}{R_v} — {I_2}R}}{{{I_2}{R_v} — U}}\]
\[{\rm E} = \frac{{U{I_2}\left( {{R_v} — R} \right)}}{{{I_2}{R_v} — U}}\]
Подставим данные в полученную формулу и посчитаем ответ:
\[{\rm E} = \frac{{1,37 \cdot 0,132 \cdot \left( {20 — 10} \right)}}{{0,132 \cdot 20 — 1,37}} = 1,424\;В = 1424\;мВ\]
Ответ: 1424 мВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.23 Щелочной аккумулятор создает силу тока 0,8 А, если его замкнуть на сопротивление 1,5 Ом
7.2.25 Два источника тока с ЭДС 2 и 1,2 В, внутренними сопротивлениями 0,5 и 1,5 Ом соответственно
7.2.26 Аккумулятор подключен для зарядки к сети с напряжением 12,5 В. Внутреннее сопротивление

 icodepro.ru
icodepro.ru
Зачем вообще понадобился 3 вывод