Условие задачи:
В рентгеновской трубке пучок электронов с плотностью тока 0,2 А/мм2 попадает на участок скошенного торца металлического стержня. Площадь этого участка 1 см2, а ось пучка образует угол 30° с поверхностью торца. Определить ток в стержне.
Задача №7.1.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(j=0,2\) А/мм2, \(S=1\) см2, \(\alpha=30^\circ\), \(I-?\)
Решение задачи:
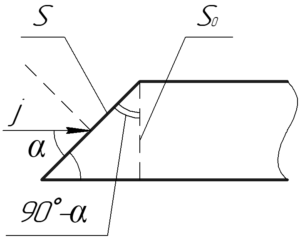 Силу тока в стержне \(I\) можно определить через плотность тока \(j\) и площадь поперечного сечения стержня \(S_0\) (обратите внимание, что это не площадь скошенного торца \(S\)):
Силу тока в стержне \(I\) можно определить через плотность тока \(j\) и площадь поперечного сечения стержня \(S_0\) (обратите внимание, что это не площадь скошенного торца \(S\)):
\[I = j{S_0}\;\;\;\;(1)\]
По теореме об ортогональной проекции площадь сечения стержня \(S_0\) связана с площадью скошенного торца \(S\) по такой формуле (также смотрите рисунок к задаче):
\[{S_0} = S \cdot \cos \left( {90^\circ — \alpha } \right)\]
\[{S_0} = S \cdot \sin \alpha \;\;\;\;(2)\]
Подставив (2) в (1), получим окончательное решение задачи:
\[I = jS\sin \alpha \]
Посчитаем ответ:
\[I = 0,2 \cdot {10^6} \cdot {10^{ — 4}} \cdot \sin 30^\circ = 10\;А\]
Ответ: 10 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.1.29 Какой ток покажет амперметр, если R1=1,25 Ом, R2=1 Ом, R3=3 Ом, R4=7 Ом, напряжение
7.1.31 За какое время в металлическом проводнике с током 32 мкА через поперечное сечение
7.1.32 Анодный ток в радиолампе равен 16 мА. Сколько электронов попадает на анод лампы

 icodepro.ru
icodepro.ru
Надеюсь, вы знаете, что косинус 30* = Sqrt(3)/2
Решение откорректировано, спасибо за замечание