Условие задачи:

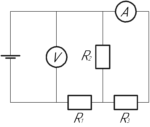В схеме, изображенной на рисунке, $R_1=5$ Ом, $R_2=6$ Ом, $R_3=3$ Ом, сопротивлением амперметра и подводящих проводов можно пренебречь. Вольтметр показывает 2,1 В. Каково показание амперметра?

Задача №7.5.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$R_1=5$ Ом, $R_2=6$ Ом, $R_3=3$ Ом, $U=2,1$ В, $I_1-?$

Решение задачи:

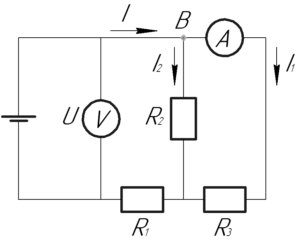Если посмотреть на схему, то видно, что ток $I$ разделяется в узле B на два тока $I_1$ и $I_2$:

$$I = {I_1} + {I_2}\;\;\;\;(1)$$

Также на схеме видно, что сопротивление $R_2$ соединено параллельно с амперметром и сопротивлением $R_3$, то есть они находятся под одинаковым напряжением. Так как в условии сказано, что сопротивлением амперметра можно пренебречь, то имеем право записать следующее:

$${I_1}{R_3} = {I_2}{R_2}$$

Выразим отсюда силу тока $I_2$:

$${I_2} = {I_1}\frac{{{R_3}}}{{{R_2}}}\;\;\;\;(2)$$

Подставим выражение (2) в формулу (1):

$$I = {I_1} + {I_1}\frac{{{R_3}}}{{{R_2}}}$$

$$I = \frac{{{I_1}\left( {{R_2} + {R_3}} \right)}}{{{R_2}}}$$

Откуда искомая сила тока на амперметре $I_1$ равна:

$${I_1} = \frac{{I{R_2}}}{{{R_2} + {R_3}}}\;\;\;\;(3)$$

Отлично, значит теперь нужно найти общую силу тока $I$, сделать это можно элементарно по закону Ома для участка цепи:

$$I = \frac{U}{R}\;\;\;\;(4)$$

Здесь $R$ — общее сопротивление цепи, отстоящей от ветви с вольтметром справа. Эта цепь состоит из двух параллельно соединенных сопротивлений $R_2$ и $R_3$, которые в свою очередь соединены последовательно с сопротивлением $R_1$. Поэтому нетрудно понять, что сопротивление $R$ получится определить по формуле:

$$R = {R_1} + \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}}$$

Если привести под общий знаменатель, получим:

$$R = \frac{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}{{{R_2} + {R_3}}}$$

Полученное выражение подставим в формулу (4):

$$I = \frac{{U\left( {{R_2} + {R_3}} \right)}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}$$

А это выражение подставим в формулу (3):

$${I_1} = \frac{{U\left( {{R_2} + {R_3}} \right)}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}} \cdot \frac{{{R_2}}}{{{R_2} + {R_3}}}$$

$${I_1} = \frac{{U{R_2}}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}$$

Отлично, задача решена в общем виде. Подставим численные данные в формулу и посчитаем численный ответ:

$${I_1} = \frac{{2,1 \cdot 6}}{{5 \cdot 6 + 5 \cdot 3 + 6 \cdot 3}} = 0,2\;А$$

Ответ: 0,2 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.5.47 По проводнику сопротивлением 4 Ом в течение 2 минут прошло 500 Кл электричества
7.5.49 Вольтметр, внутреннее сопротивление которого равно 50 кОм, подключенный к источнику
7.5.50 Определите показание амперметра в электрической цепи, изображенной на рисунке