Условие задачи:
При падении света на поверхность скипидара из вакуума угол падения равен 45°, а угол преломления 30°. Найти скорость распространения света в скипидаре.
Задача №10.2.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=45^\circ\), \(\beta=30^\circ\), \(\upsilon-?\)
Решение задачи:
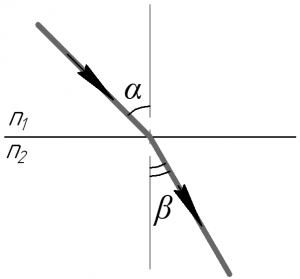 Показатель преломления данной среды относительно вакуума называется абсолютным показателем преломления данной среды \(n\), его можно определить как отношение скорости света в вакууме \(c\), равной 3·108 м/с, к скорости света в данной среде \(\upsilon\). Применительно к скипидару будет справедливо записать:
Показатель преломления данной среды относительно вакуума называется абсолютным показателем преломления данной среды \(n\), его можно определить как отношение скорости света в вакууме \(c\), равной 3·108 м/с, к скорости света в данной среде \(\upsilon\). Применительно к скипидару будет справедливо записать:
\[n_2 = \frac{c}{\upsilon}\]
Откуда выразим искомую скорость света в скипидаре \(\upsilon\):
\[\upsilon = \frac{c}{n_2}\;\;\;\;(1)\]
Запишем закон преломления света (также известен как закон преломления Снеллиуса):
\[{n_1}\sin \alpha = {n_2}\sin \beta \]
Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления вакуума \(n_1\) равен 1.
Выразим отсюда показатель преломления скипидара \(n_2\):
\[{n_2} = \frac{{{n_1}\sin \alpha }}{{\sin \beta }}\;\;\;\;(2)\]
Подставим выражение (2) в формулу (1):
\[\upsilon = \frac{{c\sin \beta }}{{{n_1}\sin \alpha }}\]
Численный ответ равен:
\[\upsilon = \frac{{3 \cdot {{10}^8} \cdot \sin 30^\circ }}{{1 \cdot \sin 45^\circ }} = 2,12 \cdot {10^8}\;м/с\]
Ответ: 2,12·108 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.2.10 Показатель преломления света относительно воды равен 1,16. Найти скорость света в воде
10.3.1 Угол падения луча света на границу стекло-воздух равен 30°. Каков угол преломления?
10.3.2 Под каким углом следует направить луч на поверхность стекла, чтобы угол преломления

 icodepro.ru
icodepro.ru