Условие задачи:

Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила лежавшую на двух столах (как на опорах) доску массой 0,27 кг. При этом доска подпрыгнула на высоту 0,2 м над уровнем столов. Какое количество теплоты выделилось при прохождении пули через доску?

Задача №2.8.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=9\) г, \(\upsilon_0=200\) м/с, \(M=0,27\) кг, \(h=0,2\) м, \(Q-?\)

Решение задачи:

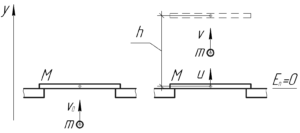В задачах на столкновения обычно применяют сразу два закона: закон сохранения энергии и закон сохранения импульса. Обратите внимание, что удар был неупругим, поскольку выделилась энергия \(Q\). Запишем указанные законы для моментов до и после удара.

\[\left\{ \begin{gathered}
\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + \frac{{M{u^2}}}{2} + Q \;\;\;\;(1)\hfill \\
m{\upsilon _0} = m\upsilon + Mu \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Выразим из (1) искомое количество теплоты \(Q\):

\[Q = \frac{m}{2}\left( {\upsilon _0^2 — {\upsilon ^2}} \right) — \frac{{M{u^2}}}{2}\;\;\;\;(3)\]

Из выражения (2) выразим скорость пули после удара \(\upsilon\):

\[m\upsilon  = m{\upsilon _0} — Mu\]

\[\upsilon  = {\upsilon _0} — \frac{M}{m}u\]

Полученную формулу подставим в (3), тогда:

\[Q = \frac{m}{2}\left( {\upsilon _0^2 — {{\left( {{\upsilon _0} — \frac{M}{m}u} \right)}^2}} \right) — \frac{{M{u^2}}}{2}\;\;\;\;(4)\]

Нам неизвестна скорость доски \(u\) после удара. Но мы можем найти её, если применить закон сохранения энергии для доски после удара и когда она будет на высоте \(h\).

\[\frac{{M{u^2}}}{2} = Mgh\]

\[u = \sqrt {2gh} \]

Последнее подставим в (4):

\[Q = \frac{m}{2}\left( {\upsilon _0^2 — {{\left( {{\upsilon _0} — \frac{M}{m}\sqrt {2gh} } \right)}^2}} \right) — \frac{{M{{\left( {\sqrt {2gh} } \right)}^2}}}{2}\]

Как можно видеть, в этой формуле нет неизвестных, то есть уже можно посчитать ответ. Но давай попробуем упростить её, раскрыв квадрат, а потом и все скобки.

\[Q = \frac{m}{2}\left( {\upsilon _0^2 — \upsilon _0^2 + \frac{{2M{\upsilon _0}}}{m}\sqrt {2gh}  — \frac{{2{M^2}gh}}{{{m^2}}}} \right) — Mgh\]

\[Q = \frac{m}{2}\left( {\frac{{2M{\upsilon _0}}}{m}\sqrt {2gh}  — \frac{{2{M^2}gh}}{{{m^2}}}} \right) — Mgh\]

\[Q = M{\upsilon _0}\sqrt {2gh}  — \frac{{{M^2}gh}}{m} — Mgh\]

\[Q = M\left( {{\upsilon _0}\sqrt {2gh}  — \frac{{Mgh}}{m} — gh} \right)\]

Так формула выглядит гораздо лучше. Давайте посчитаем ответ, предварительно переведя массу пули в систему СИ.

\[9\; г = \frac{9}{{1000}}\; кг = 0,009\; кг\]

\[Q = 0,27\left( {200\sqrt {2 \cdot 10 \cdot 0,2}  — \frac{{0,27 \cdot 10 \cdot 0,2}}{{0,009}} — 10 \cdot 0,2} \right) = 91,26\; Дж\]

Ответ: 91,26 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.39 Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка