Условие задачи:

Расстояние между двумя опорами 8 м. На эти опоры положили горизонтальную балку массы 100 кг и длины 10 м так, чтобы 2 м балки выступали за левую опору. Чему равна сила давления балки на правую опору?

Задача №3.1.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=8\) м, \(m=100\) кг, \(L=10\) м, \(F_2-?\)

Решение задачи:

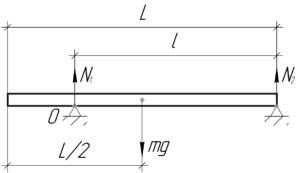Согласно третьему закону Ньютона сила давления балки на правую опору \(F_2\) равна по модулю (величине) силе реакции опоры \(N_2\).

\[{F_2} = {N_2}\]

Рассмотрим балку, лежащую на двух опорах. На неё действуют три силы: сила тяжести самой балки \(mg\) и две силы реакции \(N_1\) и \(N_2\). Балка находится в равновесии, запишем правило моментов относительно точки O — в таком случае момент силы реакции \(N_1\) равен нулю.

\[mg \cdot \left( {\frac{L}{2} — \left( {L — l} \right)} \right) = {N_2} \cdot l\]

Выразим силу \(N_2\):

\[{N_2} = \frac{{mg}}{l}\left( {\frac{L}{2} — L + l} \right)\]

\[{N_2} = \frac{{mg}}{l}\left( {l — \frac{L}{2}} \right)\]

\[{N_2} = mg\left( {1 — \frac{L}{{2l}}} \right)\]

Учитывая равенство (1), имеем:

\[{F_2} = mg\left( {1 — \frac{L}{{2l}}} \right)\]

Считаем численный ответ:

\[{F_2} = 100 \cdot 10 \cdot \left( {1 — \frac{{10}}{{2 \cdot 8}}} \right) = 375\;Н\]

Ответ: 375 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.27 К вертикальной гладкой стене подвешен на тросе AB однородный шар массы M. Определите
3.1.29 Однородная балка длины 2 м и массы 1000 кг удерживается в горизонтальном положении
3.1.30 Расстояние между двумя опорами 8 м. На эти опоры положили горизонтальную