Условие задачи:

Резиновая камера содержит воздух при температуре 27° C и нормальном атмосферном давлении. На какую глубину нужно опустить камеру в воду, чтобы её объем уменьшился вдвое? Температура воды 4° C.

Задача №4.2.64 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$t_1=27^\circ$ C, $p_0=100$ кПа, $V_2=\frac{V_1}{2}$, $t_2=4^\circ$ C, $h-?$

Решение задачи:

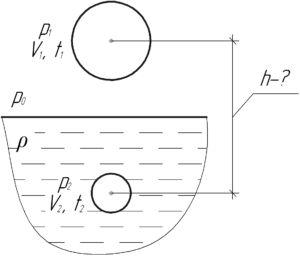Давление воздуха в резиновой камере всегда равно внешнему давлению. Поэтому, когда резиновая камера находится в воздухе, то воздух внутри неё оказывает атмосферное давление, а если она находится в воде на глубине $h$ — давление воздуха внутри камеры будет равно давлению воды на этой искомой глубине $h$.

$$\left\{ \begin{gathered} {p_1} = {p_0} \;\;\;\;(1)\hfill \\ {p_2} = {p_0} + \rho gh \;\;\;\;(2)\hfill \\ \end{gathered} \right.$$

Здесь $\rho$ — плотность воды, равная 1000 кг/м³.

Если опустить резиновую камеру на некоторую глубину в воду, то её объем уменьшится (об этом сказано в условии), а температура воздуха в камере станет равной температуре воды.

Запишем объединенный газовый закон (уравнение Клапейрона):

$$\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}$$

Из этого равенства выразим $p_2$:

$${p_2} = {p_1}\frac{{{V_1}{T_2}}}{{{V_2}{T_1}}}$$

Подставим в это равенство выражения (1) и (2) и учтём, что по условию $V_2=\frac{V_1}{2}$, тогда:

$${p_0} + \rho gh = {p_0}\frac{{2{V_1}{T_2}}}{{{V_1}{T_1}}}$$

$${p_0} + \rho gh = {p_0}\frac{{2{T_2}}}{{{T_1}}}$$

Осталось только выразить искомую глубину $h$:

$$\rho gh = {p_0}\left( {\frac{{2{T_2}}}{{{T_1}}} — 1} \right)$$

$$h = \frac{{{p_0}}}{{\rho g}}\left( {\frac{{2{T_2}}}{{{T_1}}} — 1} \right)$$

Переведём данные в условии температуры в систему СИ:

$$27^\circ\;C  = 300\;К$$

$$4^\circ\;C  = 277\;К$$

$$h = \frac{{100 \cdot {{10}^3}}}{{1000 \cdot 10}}\left( {\frac{{2 \cdot 277}}{{300}} — 1} \right) = 8,47\;м = 847\;см$$

Ответ: 847 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.63 В двух сосудах находится одинаковое количество одного и того же газа. В первом сосуде
4.2.65 В баллоне объемом 10 л находится кислород, масса которого 12,8 г. Давление в баллоне
4.2.66 Баллон содержит 0,3 кг гелия. Абсолютная температура в баллоне уменьшилась на 10%