icodepro.ruУсловие задачи:
Шар массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку шар стал двигаться в противоположном направлении со скоростью 4 м/с. Чему равно изменение импульса шара в результате удара?
Задача №2.1.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=0,1\) кг, \(\upsilon_0=5\) м/с, \(\upsilon=4\) м/с, \(\Delta p-?\)
Решение задачи:
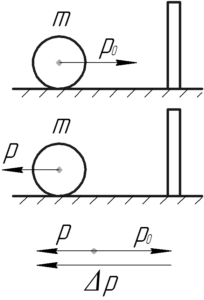Вектор изменения импульса \(\overrightarrow {\Delta p}\) равен разности векторов конечного импульса \(\overrightarrow p\) и начального импульса \(\overrightarrow {{p_0}}\).
\[\overrightarrow {\Delta p} = \overrightarrow p — \overrightarrow {{p_0}} \]
Перенесем начала векторов начального и конечного импульсов в одну точку. Соединив концы этих векторов получаем вектор \(\overrightarrow {\Delta p}\), направление которого выбирается так, чтобы выполнялось условие:
\[\overrightarrow p = \overrightarrow {\Delta p} + \overrightarrow {{p_0}} \]
Результат вы можете видеть на рисунке. Почему важно уметь определять направление изменения импульса? Дело в том, что второй закон Ньютона в общем виде выглядит так:
\[\overrightarrow F = \frac{{\overrightarrow {\Delta p} }}{{\Delta t}}\]
Получается что результирующая сила, действующая на тело, направлена в ту же сторону, что и вектор изменения импульса.
По рисунку видно, что модуль вектора изменения импульса (то есть его численное значение), равен сумме модулей начального и конечного импульсов.
Вообще, импульс — это физическая величина, равная произведению массы тела на его скорость. Суммируя все вышесказанное, запишем:
\[\Delta p = {p_0} + p\]
\[\Delta p = m{\upsilon _0} + m\upsilon = m\left( {{\upsilon _0} + \upsilon } \right)\]
\[\Delta p = 0,1\left( {5 + 4} \right) = 0,9\; кг \cdot м/с\]
Ответ: 0,9 кг · м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.18 С какой силой давит тело массой 2 кг на пол лифта, поднимающегося с ускорением
2.1.20 Автомобиль массой 2 т, двигаясь равноускоренно, через 4 с достиг скорости 2 м/с
2.1.21 На тело массой 15 кг, лежащее на земле, действует направленная вверх сила 45 Н
В задаче говорится о движении шара…
На рисунке шар ещё и катится по поверхности..
Странная задача?
Задача решена для МАТЕРИАЛЬНОЙ ТОЧКИ…
Так надо и говорить…
Материальная точка массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку она стала двигаться в противоположном направлении со скоростью 4 м/с. Чему равно изменение импульса материальной точки в результате удара?
ВОПРОС:
а за счет чего материальная точка потеряла часть импульса?
Почему мы ищем скаляр, а не вектор? Разве правильно не так: dp=p-p0=m(v2-v1)=-0.1 kg*m/s?
ага, кажется, разобрался. импульс до столкновения 0.5, после меняется на dp=-0.9 или по модулю 0.9, 0.5-0.9=-0.4 — направление меняется. правильно рассуждаю?
Абсолютно верно
Потому что импульс — это векторная величина. В задаче мы находим модуль вектора, то есть его длину.
Расскажите подробнее, как определяется направление вектора «дельта p»?
Вы знаете направление вектора \(\overrightarrow p \), также Вы знаете направление начального вектора \(\overrightarrow {{p_0}} \). Вектор \(\overrightarrow {\Delta p} \) равен разности указанных векторов, то есть \(\overrightarrow {\Delta p} = \overrightarrow p — \overrightarrow {{p_0}} \).
Чтобы найти разность векторов, нужно использовать правило треугольника (как я и сделал в решении, смотри рисунок): из одной точки откладываем оба вектора (начальный \(\overrightarrow {{p_0}} \) и конечный \(\overrightarrow p \)). Тогда вектор, начало которого совпадает с концом вектора \(\overrightarrow {{p_0}} \), а конец – с концом вектора \(\overrightarrow p \)), и будет искомым вектором \(\overrightarrow {\Delta p} \).