icodepro.ruУсловие задачи:
Скорость движения автомобиля от времени задана уравнением \(\upsilon=3+2t\). Какой путь пройдет автомобиль за 6 с?
Задача №1.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=3+2t\), \(t=6\) с, \(S-?\)
Решение задачи:
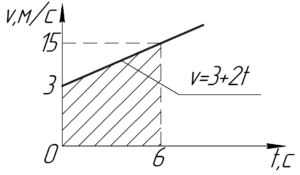Напомним тот факт, что площадь фигуры под графиком изменения скорости численно показывает пройденный путь. Поэтому построим график уравнения, данного в условии.
Полученная фигура — трапеция (на рисунке заштрихована), её площадь рассчитывается как полупроизведение суммы оснований на высоту.
\[S = \frac{1}{2}\left( {15 + 3} \right) \cdot 6 = 54\; м \]
Ответ: 54 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.23 Тормозной путь автомобиля, двигавшегося со скоростью 30 км/ч, равен 7,2 м. Чему
1.3.25 По одному направлению из одной точки одновременно начали двигаться два тела
1.3.26 Скорость движения тела, равная 10 м/с, за 17 с уменьшилась в 5 раз. Определить
А откуда 15 взяли ?
Вопрос, а почему 54? Мы ведь используем s=v0+at^2/2 и выходит 39. Или нет?
Вы в формуле забыли \(t\) после начальной скорости \(\upsilon_0\). Формула должна выглядеть так:\[S = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]\[S = 3 \cdot 6 + \frac{{2 \cdot {6^2}}}{2} = 54\;м\]
А если взять первообразную, а затем подставить значение времени?
Ну давайте попробуем\[\int\limits_{{t_0}}^{{t_1}} {\upsilon dt = } \int\limits_{{t_0}}^{{t_1}} {\left( {3 + 2t} \right)dt = } \left. {3t + {t^2}} \right|_{{t_0} = 0}^{{t_1} = 6} = \left( {3 \cdot 6 + {6^2}} \right) — \left( {3 \cdot 0 + {0^2}} \right) = 54\]Как Вы видите, получается точно такой же ответ