Решение: Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде

Условие задачи:

Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде. С какой силой давит на дно сосуда шар, если в воздухе он весит 6 Н?

Задача №3.3.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_п=0,5V\), \(P_в=6\) Н, \(P-?\)

Решение задачи:

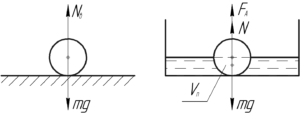Вес тела – это сила, с которой оно действует на опору (или на подвес), то есть она численно равна силе реакции опоры. Тогда понятно, что вес тела в воздухе и воде (когда тело погружено в неё наполовину) можно определить по следующим формулам:

\[\left\{ \begin{gathered}
{P_в} = mg \hfill \\
P = mg – {F_А} \hfill \\
\end{gathered} \right.\]

В обеих формулах распишем массу (по формуле \(m= \rho V\)) и силу Архимеда (\(F_А = \rho_в gV_п = 0,5 \rho_в gV\)):

\[\left\{ \begin{gathered}
{P_в} = \rho Vg \hfill \\
P = \rho Vg – 0,5{\rho _в}gV \hfill \\
\end{gathered} \right.\]

Перепишем нижнюю формулу в более удобном виде:

\[\left\{ \begin{gathered}
{P_в} = \rho Vg \hfill \\
P = \left( {\rho – 0,5{\rho _в}} \right)Vg \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда получим:

\[\frac{P}{{{P_в}}} = \frac{{\rho – 0,5{\rho _в}}}{\rho }\]

\[P = {P_в}\frac{{\rho – 0,5{\rho _в}}}{\rho }\]

\[P = {P_в}\left( {1 – \frac{{{\rho _в}}}{{2\rho }}} \right)\]

Задача решена в общем виде. Учитывая, что плотность дерева \(\rho\) равна 700 кг/м³, а плотность воды \(\rho_в\) – 1000 кг/м³, можно произвести расчет ответа.

\[P = 6 \cdot \left( {1 – \frac{{1000}}{{2 \cdot 700}}} \right) = 1,71\;Н\]