icodepro.ruУсловие задачи:
Два деревянных шара одинакового объема, полностью находящиеся в жидкости, соединены нитью и поднимаются равномерно и вертикально один над другим. Пренебрегая силами сопротивления жидкости, определите силу натяжения нити, если массы шаров равны 2 и 4 кг.
Задача №3.3.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=2\) кг, \(m_2=4\) кг, \(T-?\)
Решение задачи:
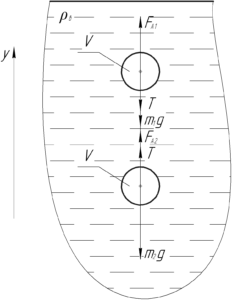Шар, имеющий меньшую массу \(m_1\), находится выше шара с массой \(m_2\).
Все силы, действующие на оба шара, показаны на схеме. Так как они движутся равномерно, запишем первый закон Ньютона для каждого шара в проекции на ось \(y\):
\[\left\{ \begin{gathered}
{F_{А1}} – {m_1}g – T = 0 \hfill \\
T + {F_{А2}} – {m_2}g = 0 \hfill \\
\end{gathered} \right.\]
Вычтем из первого равенства второе, тогда получим:
\[{F_{А1}} – {m_1}g – T – T – {F_{А2}} + {m_2}g = 0\]
Очевидно, что выталкивающие силы, действующие на шары, одинаковы, так как они погружены в одну жидкость, и их объемы одинаковы:
\[{F_{А1}} = {F_{А2}}\]
Тогда имеем:
\[2T = \left( {{m_2} – {m_1}} \right)g\]
\[T = 0,5\left( {{m_2} – {m_1}} \right)g\]
Задача решена в общем виде. Посчитаем численный ответ:
\[T = 0,5 \cdot \left( {4 – 2} \right) \cdot 10 = 10\;Н\]
Ответ: 10 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.50 Шарик для игры в настольный теннис радиусом 15 мм и массой 5 г погружен в воду
3.3.52 В сосуде находятся две несмешивающиеся жидкости с различными плотностями
3.3.53 Плотность воды 1000 кг/м3, а плотность пробки 200 кг/м3. Пробковый шар массы 100 г
Ещё хотелось бы, чтоб на сайте была возможность редактирования отправленных вопросов как в контакте (например, мне нужно уточнение внести: как решалась бы задача (в общем виде (уточнение)) если б вопрос был сформулирован по другому: Учитывая силы сопротивления жидкости, определите силу натяжения нити, если массы шаров равны 2 и 4 кг?
Хорошо, я учту Ваше пожелание, постараюсь это реализовать
Здравствуйте. А как решалась бы задача если б вопрос был сформулирован по другому: Учитывая силы сопротивления жидкости, определите силу натяжения нити, если массы шаров равны 2 и 4 кг?
При данном условии такую задачу едва ли можно было решить (это моё мнение, мне нужно видеть текст задачи). Дело в том, что сила сопротивления в жидкости описывается некоторым законом (например \({F_с} = k\upsilon \)). Получается , что Вам должны дать в условии коэффициент сопротивления \(k\) и скорость \(\upsilon\), либо предоставить некоторые данные, которые позволят определить эти неизвестные.
В любом случае задача бы решалась теми же методами механики (законы Ньютона), возможно пришлось бы применять методы кинематики (например, если было бы дано пройденное расстояние \(S\) и время \(t\)).
Пришлите сюда полный текст задачи (если Вы, конечно, не занимаетесь сочинением задачи), я Вам покажу её решение.
Уточнение: вы же задачи сначала решаете в общем виде: мне достаточно показать, как решалась бы задача в общем виде, если б вопрос был сформулирован по другому: учитывая силы сопротивления жидкости, определите силу натяжения нити, если массы шаров равны 2 и 4 кг? Допустим, известно всё, что должны дать в условии: к примеру коэффициент сопротивления и скорость (любые значения можно задать, главное увидеть, как в общем виде будет решаться).
Первый закон Ньютона запишется в следующем виде:
\[\left\{ \begin{gathered}
{F_{А1}} – {m_1}g – T – {F_{с1}} = 0 \hfill \\
T + {F_{А2}} – {m_2}g – {F_{с2}} = 0 \hfill \\
\end{gathered} \right.\]Также вычитаем из первого равенства второе:\[{F_{А1}} – {m_1}g – T – {F_{с1}} – T – {F_{А2}} + {m_2}g + {F_{с2}} = 0\]Силы Архимеда и силы сопротивления, действующие на оба шара, должны быть равны, поэтому:\[ – {m_1}g – 2T + {m_2}g = 0\]Откуда имеем:\[T = \frac{{\left( {{m_2} – {m_1}} \right)g}}{2}\]Получается, что от наличия силы сопротивления ответ не изменится
в ответе не 10Н .а 2Н
Вероятно Вы смотрите задачу с другим условием
А как шары одинакого объема и материла имеют разную массу? Это вроде как анрил
Один из шаров может иметь полость внутри себя