К телу, сделанному из пробки, привязали веревку, другой конец которой закрепили

Условие задачи:

К телу, сделанному из пробки, привязали веревку, другой конец которой закрепили на дне озера. При этом 0,6 всего объема тела оказалось в воде. Определить силу натяжения веревки, если масса тела 1 кг.

Задача №3.3.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_{п}=0,6V\), \(m=1\) кг, \(T-?\)

Решение задачи:

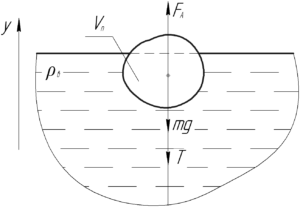На тело действует сила натяжения веревки \(T\), сила тяжести \(mg\) и сила Архимеда \(F_{А}\). Поскольку оно находится в равновесии, то запишем первый закон Ньютона в проекции на ось \(y\):

\[{F_А} – mg – T = 0\]

\[T = {F_А} – mg\;\;\;\;(1)\]

Массу тела \(m\) можно найти как произведение его плотности \(\rho\) (плотность пробки \(\rho=200\) кг/м³) на полный объем \(V\):

\[m = \rho V\;\;\;\;(2)\]

Сила Архимеда \(F_А\) определяется по такой формуле:

\[{F_А} = {\rho _в}g{V_п} = 0,6{\rho _в}gV\;\;\;\;(3)\]

В этой формуле \(\rho_в\) – плотность воды, равная 1000 кг/м³. Подставим выражения (2) и (3) в равенство (1):

\[T = 0,6{\rho _в}gV – \rho Vg = \left( {0,6{\rho _в} – \rho } \right)gV\]

Единственную неизвестную величину в этой формуле – объем \(V\) – найдем по такой формуле:

\[V = \frac{m}{\rho }\]

В итоге получим такое решение задачи в общем виде:

\[T = \left( {0,6{\rho _в} – \rho } \right)\frac{{mg}}{\rho }\]

Подставим данные задачи и посчитаем ответ:

\[T = \left( {0,6 \cdot 1000 – 200} \right)\frac{{1 \cdot 10}}{{200}} = 20\;Н\]

Ответ: 20 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.12 Дубовый шар лежит в сосуде с водой, причем половина его находится в воде. С какой
3.3.14 Кусок дерева плавает в воде, погружаясь на 0,75 своего объема. Какова плотность
3.3.15 Кусок металла массой 0,78 кг весит в воде 6,8 Н, а в бензине – 7,1 Н. Определить