К тросу длиной 3 м, концы которого закреплены на одной высоте, на расстоянии 1 м

Условие задачи:

К тросу длиной 3 м, концы которого закреплены на одной высоте, на расстоянии 1 м от точек закрепления подвешены два груза массой 1 кг каждый. Провисание средней горизонтальной части троса составило 10 см. Найти силы натяжения троса на каждом из трёх участков?

Задача №3.1.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=3\) м, \(l=1\) м, \(m=1\) кг, \(h=10\) см, \(T_1, T_2-?\)

Решение задачи:

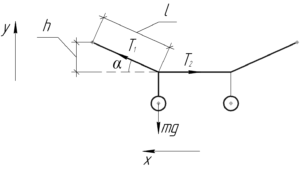По схеме видно, что достаточно рассмотреть равновесие одного из грузов, поскольку схема симметрична.

Запишем первое условие равновесия в проекции на оси \(x\) и \(y\) для левого груза:

\[\left\{ \begin{gathered}
{T_1} \cdot \cos \alpha = {T_2} \hfill \\
{T_1} \cdot \sin \alpha = mg \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда:

\[tg\alpha  = \frac{{mg}}{{{T_2}}}\]

\[{T_2} = \frac{{mg}}{{tg\alpha }}\;\;\;\;(1)\]

Из первого равенства системы следует, что:

\[{T_1} = \frac{{{T_2}}}{{\cos \alpha }}\]

Учитывая (1), эта формула примет вид:

\[{T_1} = \frac{{mg}}{{\sin \alpha }}\]

Осталось только найти синус и тангенс угла \(\alpha\). Очевидно, что:

\[\sin \alpha  = \frac{h}{l}\]

\[tg\alpha  = \frac{h}{{\sqrt {{l^2} – {h^2}} }}\]

В итоге:

\[{T_1} = \frac{{mgl}}{h}\]

\[{T_2} = \frac{{mg\sqrt {{l^2} – {h^2}} }}{h}\]

Переведем величину провисания \(h\) в систему СИ и произведем вычисление ответа.

\[10\;см = \frac{{10}}{{100}}\;м = 0,1\;м\]

\[{T_1} = \frac{{1 \cdot 10 \cdot 1}}{{0,1}} = 100\;Н\]

\[{T_2} = \frac{{1 \cdot 10\sqrt {{1^2} – {{0,1}^2}} }}{{0,1}} = 99,5\;Н\]

Ответ: 100 Н; 99,5 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.7 Два одинаковых шарика, масса и радиусы которых равны соответственно 100 г и 3 см
3.1.9 Шар массой 5 кг опирается на две гладкие плоскости, образующие угол, причем
3.1.10 В ящике находится шар массой 3 кг. Ящик наклоняют так, что его дно составляет