На аэростат в горизонтальном направлении действует ветер с силой 3000 Н. Натяжение

Условие задачи:

На аэростат в горизонтальном направлении действует ветер с силой 3000 Н. Натяжение троса 5000 Н. Определить натяжение троса в безветренную погоду.

Задача №3.1.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(F_1=3000\) Н, \(T_1=5000\) Н, \(T-?\)

Решение задачи:

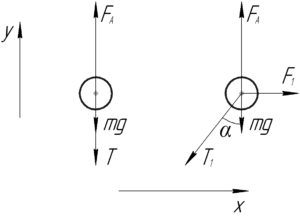В безветренную погоду на аэростат действуют три силы: сила Архимеда \(F_А\), сила тяжести \(mg\) и сила натяжения троса \(T\). Запишем первое условие равновесия в проекции на ось \(y\) (левая часть схемы):

\[{F_А} – mg – T = 0\]

\[T = {F_А} – mg\;\;\;\;(1)\]

Если же дует ветер, при этом он действует на аэростат с силой \(F_1\), то аэростат отклонится так, что трос станет наклонен под некоторым углом \(\alpha\) к вертикали. Это происходит из-за того, что аэростат под действием ветра придёт в движение и будет двигаться до тех пор, пока проекция силы натяжения \(T_1\) на ось \(x\) не уравновесит силу ветра \(F_1\). Запишем первое условие равновесия в проекции на обе оси (правая часть схемы):

\[\left\{ \begin{gathered}
{F_А} – mg – {T_1}\cos \alpha = 0 \hfill \\
{F_1} = {T_1}\sin \alpha \hfill \\
\end{gathered} \right.\]

Так как сила Архимеда \(F_А\) и сила тяжести \(mg\) не меняются, то применив ранее полученное равенство (1), получим:

\[\left\{ \begin{gathered}
T = {T_1}\cos \alpha \hfill \\
{F_1} = {T_1}\sin \alpha \hfill \\
\end{gathered} \right.\]

Выразим из нижнего равенство синус угла \(\alpha\):

\[\sin \alpha  = \frac{{{F_1}}}{{{T_1}}}\]

Основное тригонометрическое тождество гласит, что:

\[{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\]

\[\cos \alpha  = \sqrt {1 – {{\sin }^2}\alpha } \]

Тогда:

\[\cos \alpha  = \sqrt {1 – {{\left( {\frac{{{F_1}}}{{{T_1}}}} \right)}^2}} \]

В итоге:

\[T = {T_1}\sqrt {1 – {{\left( {\frac{{{F_1}}}{{{T_1}}}} \right)}^2}} \]

Если внести \(T_1\) под знак корня, то получим окончательную формулу:

\[T = \sqrt {T_1^2 – F_1^2} \]

Считаем ответ:

\[T = \sqrt {{{5000}^2} – {{3000}^2}}  = 4000\;Н\]

Ответ: 4000 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.2 На тело действуют силы 4 и 5 Н, направленные под углом 90 градусов друг к другу
3.1.4 Какую силу необходимо приложить, чтобы приподнять за один конец бревно
3.1.5 Шар массой 6 кг висит на веревке, прикрепленной к гладкой стене. С какой силой шар