На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена

Условие задачи:

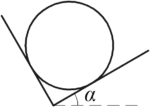На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена под углом \(\alpha=30^\circ\), лежит однородный шар массой 10 кг. Найти силу давления шара на каждую плоскость. Трением пренебречь.

Задача №3.1.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(m=10\) кг, \(F_1, F_2 – ?\)

Решение задачи:

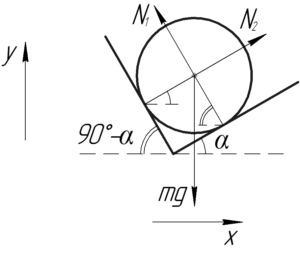Шар находится в покое под действием трех сил: силы тяжести \(mg\) и двух сил реакции \(N_1\) и \(N_2\). Запишем первое условие равновесия в проекции на координатные оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
{N_2} \cdot \cos \alpha = {N_1} \cdot \cos \left( {90^\circ – \alpha } \right) \hfill \\
{N_2} \cdot \sin \alpha + {N_1} \cdot \sin \left( {90^\circ – \alpha } \right) = mg \hfill \\
\end{gathered} \right.\]

Из тригонометрии известно, что \(\sin \alpha  = \cos \left( {90^\circ  – \alpha } \right)\) и \(\cos \alpha  = \sin \left( {90^\circ  – \alpha } \right)\), поэтому:

\[\left\{ \begin{gathered}
{N_2} \cdot \cos \alpha = {N_1} \cdot \sin \alpha \;\;\;\;(1)\hfill \\
{N_2} \cdot \sin \alpha + {N_1} \cdot \cos \alpha = mg \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Из равенства (1) выразим реакцию \(N_2\):

\[{N_2} = {N_1} \cdot tg\alpha \;\;\;\;(3)\]

Полученное выражение подставим в равенство (2):

\[{N_1} \cdot tg\alpha  \cdot \sin \alpha  + {N_1} \cdot \cos \alpha  = mg\]

\[{N_1}\left( {tg\alpha  \cdot \sin \alpha  + \cos \alpha } \right) = mg\]

\[{N_1} = \frac{{mg}}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

Используя равенство (3), найдем силу реакции \(N_2\):

\[{N_2} = \frac{{mg \cdot tg\alpha }}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

По третьему закону Ньютона сила давления на плоскость равна по модулю силе реакции опоры со стороны этой плоскости. Напомним, что эти силы равны лишь по величине, но противоположны по направлению и приложены к разным телам. Поэтому:

\[{F_1} = \frac{{mg}}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

\[{F_2} = \frac{{mg \cdot tg\alpha }}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

Посчитаем численные значения этих сил:

\[{F_1} = \frac{{10 \cdot 10}}{{tg30^\circ  \cdot \sin 30^\circ  + \cos 30^\circ }} = 86,6\;Н\]

\[{F_2} = \frac{{10 \cdot 10 \cdot tg30^\circ }}{{tg30^\circ  \cdot \sin 30^\circ  + \cos 30^\circ }} = 50\;Н\]

Ответ: 86,6 Н; 50 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.10 В ящике находится шар массой 3 кг. Ящик наклоняют так, что его дно составляет
3.1.12 При подвеске контактного провода троллейбусной сети провес опорного троса
3.1.13 Два шара, алюминиевый и цинковый, одинакового объема и радиуса 10 см скреплены