Решение: На какую высоту поднимается вода в капиллярной трубке диаметром

Условие задачи:

На какую высоту поднимается вода в капиллярной трубке диаметром 3 мм?

Задача №3.4.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d=3\) мм, \(h-?\)

Решение задачи:

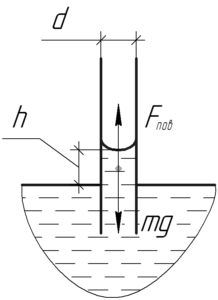Со стороны воды на линию соприкосновения с трубкой, длина которой равна \(\pi d\) (длина окружности), действует направленная вниз сила поверхностного натяжения. Её модуль которой равен:

\[F_{пов} = \pi d \cdot \sigma \]

Здесь \(\sigma\) – поверхностное натяжение воды (табличная величина), равная 72 мН/м.

Согласно третьему закону Ньютона со стороны трубки на воду действует такая же по величине сила, направленная вверх. Она и вызывает подъем воды в капилляре на такую высоту \(h\), при которой сила тяжести \(mg\), действующая на весь поднятый столб воды, равна \(F_{пов}\).

\[{F_{пов}} = mg\;\;\;\;(1)\]

Массу поднятой воды выразим через плотность \(\rho\) и объем \(V\). Объем можно найти как произведение площади поперечного сечения, равной \(\frac{{\pi {d^2}}}{4}\), на высоту \(h\).

\[m = \rho V = \rho \frac{{\pi {d^2}}}{4}h\]

Плотность воды \(\rho\) равна 1000 кг/м³.

Равенство (1) примет вид:

\[\pi d \cdot \sigma = \rho \frac{{\pi {d^2}}}{4}hg\]

\[\sigma = \rho \frac{d}{4}hg\]

\[h = \frac{{4\sigma }}{{\rho gd}}\]

Переведем диаметр трубки и поверхностное натяжение в систему СИ:

\[3\;мм = 0,003\;м\]

\[72\;мН/м = 0,072\;Н/м\]

Посчитаем ответ:

\[h = \frac{{4 \cdot 0,072}}{{1000 \cdot 10 \cdot 0,003}} = 9,6 \cdot {10^{ – 3}}\;м \approx 1\;см\]