Определить массу воды, поднявшейся по капиллярной трубке диаметром

Условие задачи:

Определить массу воды, поднявшейся по капиллярной трубке диаметром 0,5 мм.

Задача №3.4.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d=0,5\) мм, \(m-?\)

Решение задачи:

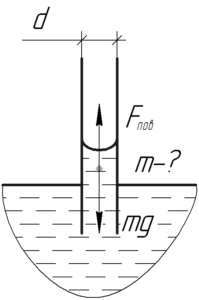На трубку вдоль линии соприкосновения с водой (её длина равна \(\pi d\)) действует сила поверхностного натяжения \(F_{пов}\). Она направлена вниз. Согласно третьему закону Ньютона на воду со стороны трубки действует такая же по величине сила, но направленная вверх. Эта сила и вызывает подъем воды в трубке. Её модуль равен:

\[{F_{пов}} = \sigma  \cdot \pi d\]

Поверхностное натяжение воды \(\sigma\) равно 72 мН/м.

Понятно, что сила тяжести поднятого столбика воды \(mg\) равна силе  поверхностного натяжения \(F_{пов}\).

\[mg = {F_{пов}}\]

\[mg = \sigma  \cdot \pi d\]

Откуда искомая масса \(m\) равна:

\[m = \frac{{\sigma \pi d}}{g}\]

Переведем диаметр трубки и поверхностное натяжение в систему СИ:

\[0,5\;мм = 5 \cdot {10^{ – 4}}\;м\]

\[72\;мН/м = 0,072\;Н/м\]

Посчитаем численный ответ к задаче:

\[m = \frac{{0,072 \cdot 3,14 \cdot 5 \cdot {{10}^{ – 4}}}}{{10}} = 1,13 \cdot {10^{ – 5}}\;кг = 11,3\;мг\]

Ответ: 11,3 мг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.4.2 В капиллярной трубке радиусом 0,5 мм жидкость поднялась на 11 мм. Определить
3.4.4 На проволочной рамке с подвижной перекладиной длиной 10 см натянута мыльная пленка
3.4.5 При лужении оловом с конца проволоки диаметром 1 мм оторвалось 20 капель олова