icodepro.ruУсловие задачи:
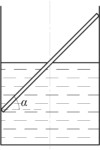Палочка массы \(m\) наполовину погружена в воду, как показано на рисунке. Угол наклона палочки к горизонту \(\alpha\). С какой силой давит на стенку цилиндрического сосуда верхний конец палочки? Трением пренебречь.
Задача №3.3.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m\), \(\alpha\), \(P-?\)
Решение задачи:
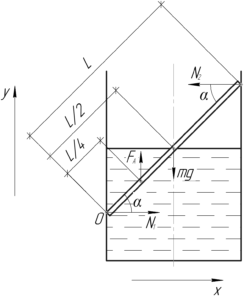Сила давления верхнего конца палочки на стенку сосуда \(P\) численно равна силе нормальной реакции опоры в этой точке \(N_2\) согласно третьему закону Ньютона.
\[P = {N_2}\]
Вообще, на палочку действуют четыре силы: сила тяжести \(mg\), выталкивающая сила воды \(F_А\) (на погруженную часть) и две силы нормальной реакции опоры \(N_1\) и \(N_2\).
Палочка находится в равновесии. Запишем первое условие равновесия (первый закон Ньютона) в проекции на обе оси координат и второе условие равновесия (правило моментов) относительно точки O. Полученные равенства запишем в виде такой системы:
\[\left\{ \begin{gathered}
{F_А} = mg \hfill \\
{N_1} = {N_2} \hfill \\
{F_А} \cdot \frac{L}{4} \cdot \cos \alpha – mg \cdot \frac{L}{2} \cdot \cos \alpha + {N_2} \cdot L \cdot \sin \alpha = 0 \hfill \\
\end{gathered} \right.\]
Из последнего равенства выразим \(N_2\):
\[{N_2} = \frac{1}{2}mg \cdot ctg\alpha – \frac{1}{4}{F_А} \cdot ctg\alpha \]
Первое равенство системы говорит о том, что \({F_А} = mg\), поэтому:
\[{N_2} = \frac{1}{2}mg \cdot ctg\alpha – \frac{1}{4}mg \cdot ctg\alpha \]
\[{N_2} = \frac{1}{4}mg \cdot ctg\alpha \]
Задачу нужно было решить в общем виде, что мы и сделали. Обратите ваше внимание, что так как \({N_1} = {N_2}\) (второе равенство в системе), значит давление нижнего конца на стенку такое же, как и давление верхнего конца.
Ответ: \(\frac{1}{4}mg \cdot ctg\alpha\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.55 Палочка массы 400 г наполовину погружена в воду, как показано на рисунке. Угол
3.4.1 На какую высоту поднимается вода в капиллярной трубке диаметром
3.4.2 В капиллярной трубке радиусом 0,5 мм жидкость поднялась на 11 мм. Определить
почему мы не берем N1. Это из за того что в данном случае он рядом с точкой опоры и расстояние будет ровняться нулю?
почему мы проектируем mg на весь y как
mg cos alpha, а не mg/sin alpha?
А,все, понял.
В данном случае это не проекция. Третье уравнение – это правило моментов относительно точки O, множитель \(\frac{L}{2}\cos \alpha \) после силы тяжести \(mg\) – это плечо этой силы относительно точки O.
Объясните пожалуйста что такое ctga?
Котангенс угла \(\alpha\), есть такая тригонометрическая функция
уточните момент силы N2
Момент силы реакции опоры N2 относительно точки O определен в решении правильно
Почему N2 проектируется с плюсом, ведь она противоположна оси X направлена
Если Вы про третье уравнение:
$${F_А} \cdot \frac{L}{4} \cdot \cos \alpha – mg \cdot \frac{L}{2} \cdot \cos \alpha + {N_2} \cdot L \cdot \sin \alpha = 0$$
то это уравнение моментов. Знак здесь определяется тем, как момент силы вращается относительно выбранной точки.
Момент силы \({N_2}\) (как и момент силы Архимеда \({F_А}\)) вращается против часовой стрелки, поэтому имеет знак “плюс”, а вот момент силы тяжести \({mg}\) вращается по часовой стрелки, поэтому у нее знак “минус”.
Здравствуйте,можете объяснить пожалуйста,почему Fa=mg?
Ведь погруженная часть тела имеет массу вдвое меньше
Не так ли?
Ну потому что на палочку (на всю палочку) вдоль вертикальной оси действуют две силы: сила Архимеда и сила тяжести, а так как она находится в равновесии, значит эти силы должны быть равны друг другу.