Плотность воды 1000 кг/м3, а плотность пробки 200 кг/м3. Пробковый шар массы 100 г

Условие задачи:

Плотность воды 1000 кг/м³, а плотность пробки 200 кг/м³. Пробковый шар массы 100 г прикреплен ко дну водоема тонкой невесомой нитью. Шар полностью погружен в воду. Чему равно натяжение нити?

Задача №3.3.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_{в}=1000\) кг/м³, \(\rho=200\) кг/м³, \(m=100\) г, \(T-?\)

Решение задачи:

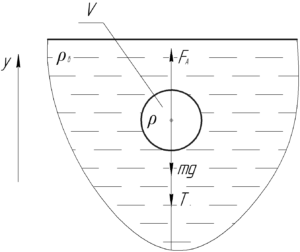Пробковый шар, очевидно, находится в состоянии равновесия, поэтому запишем первый закон Ньютона в проекции на ось \(y\):

\[{F_А} – mg – T = 0\]

\[T = {F_А} – mg\]

В полученной формуле распишем силу Архимеда \(F_{А}\) по формуле её определения и массу \(m\) через плотность \(\rho\) и объем \(V\):

\[T = {\rho _в}gV – \rho Vg\]

\[T = \left( {{\rho _в} – \rho } \right)gV\]

Поскольку масса шара дана в условии, то определить его объем не составляет трудности:

\[V = \frac{m}{\rho }\]

В итоге мы имеем такую формулу для определения силы натяжения \(T\):

\[T = \left( {{\rho _в} – \rho } \right)g\frac{m}{\rho }\]

\[T = \left( {\frac{{{\rho _в}}}{\rho } – 1} \right)mg\]

Переведем массу шара в систему СИ и посчитаем ответ:

\[100\;г = 0,1\;кг\]

\[T = \left( {\frac{{1000}}{{200}} – 1} \right) \cdot 0,1 \cdot 10 = 4\;Н\]

Ответ: 4 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.52 В сосуде находятся две несмешивающиеся жидкости с различными плотностями
3.3.54 Плотность воды 1000 кг/м3, а плотность камня 2500 кг/м3. Если не учитывать
3.3.55 Палочка массы 400 г наполовину погружена в воду, как показано на рисунке. Угол