Условие задачи:
Шар массой 5 кг опирается на две гладкие плоскости, образующие угол, причем левая образует с горизонтом угол 30°, а правая — 60°. Определить силу, с которой шар давит на левую плоскость.
Задача №3.1.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=5\) кг, \(\alpha=30^\circ\), \(\beta=60^\circ\), \(F-?\)
Решение задачи:
 По третьему закону Ньютона искомая сила давления \(F\) равна по модулю силе реакции опоры \(N_1\).
По третьему закону Ньютона искомая сила давления \(F\) равна по модулю силе реакции опоры \(N_1\).
\[F = {N_1}\;\;\;\;(1)\]
На шар действуют три силы: сила тяжести \(mg\) и две силы реакции опоры \(N_1\) и \(N_2\).
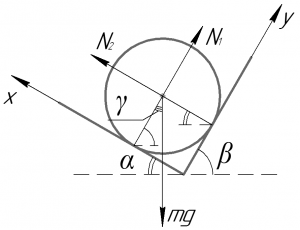
Задача решается очень просто, если оси декартовой системы координат ввести так, как показано на рисунке. В таком случае для нахождения силы реакции \(N_1\), которая равна искомой силе давления \(F\), достаточно записать первое условие равновесия в проекции на ось \(y\):
\[{N_1} = mg\cos \gamma \]
Из рисунка видно, что \(\gamma = 90^\circ — \beta\), поэтому:
\[{N_1} = mg\cos \left( {90^\circ — \beta } \right)\]
Так как \(\cos \left( {90^\circ — \beta } \right) = \sin \beta\), то:
\[{N_1} = mg\sin \beta \]
Учитывая (1), окончательно имеем:
\[F = mg\sin \beta \]
Задача решена в общем виде, осталось только посчитать численный ответ.
\[F = 5 \cdot 10 \cdot \sin 60^\circ = 43,3\;Н\]
Ответ: 43,3 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.8 К тросу длиной 3 м, концы которого закреплены на одной высоте, на расстоянии 1 м
3.1.10 В ящике находится шар массой 3 кг. Ящик наклоняют так, что его дно составляет
3.1.11 На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена

 icodepro.ru
icodepro.ru
Почему проекция Fт = mg*cosY?
Почему N1 равен mgcosY?
корректно ли найти N1 произведением mg*cos30? Ответ тот же
Да. Решение я пересмотрел, так как задачу можно решить гораздо проще
Вы вообще знаете ,сколько значит синус30 или кос30 ?
Разумеется, я полагаю у Вас возник какой-то вопрос?