Тело массой 2 кг и объемом 1 л находится в озере на глубине 5 м. Какую необходимо

Условие задачи:

Тело массой 2 кг и объемом 1 л находится в озере на глубине 5 м. Какую необходимо совершить работу для его подъема на 5 м над поверхностью воды?

Задача №3.3.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=2\) кг, \(V=1\) л, \(h_1=5\) м, \(h_2=5\) м, \(A-?\)

Решение задачи:

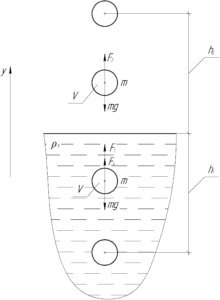Понятно, чтобы поднять тело на нужную высоту, нужно приложить некоторую внешнюю силу. При этом, чтобы работа этой силы была минимальна, тело нужно поднимать равномерно. Величину внешней силы в воде \(F_1\) и в воздухе \(F_2\) можно найти из первого закона Ньютона:

\[\left\{ \begin{gathered}
{F_1} = mg – {F_А} \hfill \\
{F_2} = mg \hfill \\
\end{gathered} \right.\]

Распишем силу Архимеда:

\[\left\{ \begin{gathered}
{F_1} = mg – {\rho _в}gV = \left( {m – {\rho _в}V} \right)g \hfill \\
{F_2} = mg \hfill \\
\end{gathered} \right.\]

Работа внешней силы при подъеме в воде и в воздухе будет положительна, так как вектор внешней силы сонаправлен с вектором перемещения. Поэтому:

\[A = {F_1}{h_1} + {F_2}{h_2}\]

Учитывая ранее полученные выражения, имеем:

\[A = \left( {m – {\rho _в}V} \right)g{h_1} + mg{h_2}\]

Посчитаем численный ответ (в системе СИ \(1\;л = 0,001\;м^3\)):

\[A = \left( {2 – 1000 \cdot 0,001} \right) \cdot 10 \cdot 5 + 2 \cdot 10 \cdot 5 = 150\;Дж\]

Ответ: 150 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.28 Стеклянный шарик объемом 0,5 см3 равномерно тонет в воде. Какое количество
3.3.30 Шарик массой 20 г всплывает с постоянной скоростью в жидкости, плотность которой
3.3.31 Шарик на нити, уравновешенный на весах, опускают в воду. Когда шарик на 0,3 своего