Условие задачи:

Свинцовая пуля пробивает доску, при этом её скорость падает с 400 до 200 м/с. Какая часть пули расплавится? Нагреванием доски пренебречь. Начальная температура пули 27 °C.

Задача №5.3.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=400\) м/с, \(\upsilon=200\) м/с, \(t_0=27^\circ\) C, \(\alpha-?\)

Решение задачи:

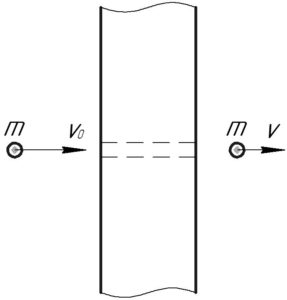Согласно закону сохранения энергии, количество теплоты \(Q\), выделившееся при пробивании доски пулей, равно изменению кинетической энергии пули, поэтому верно записать:

\[Q = \frac{{m\upsilon _0^2}}{2} — \frac{{m{\upsilon ^2}}}{2}\]

\[Q = 0,5m\left( {\upsilon _0^2 — {\upsilon ^2}} \right)\;\;\;\;(1)\]

Пусть \(m\) — полная масса пули, а \(\Delta m\) — масса расплавившейся части пули. Величину \(\alpha\) тогда следует искать по формуле:

\[\alpha = \frac{{\Delta m}}{m}\;\;\;\;(2)\]

Чтобы расплавить часть пули массой \(\Delta m\), необходимо сначала всю пулю массой \(m\) нагреть до температуры плавления (\(t_п=327^\circ\) C). Учитывая, что нагреванием доски можно пренебречь, количество теплоты \(Q\) также можно выразить следующим образом:

\[Q = cm\left( {{t_п} — {t_0}} \right) + \lambda \Delta m\;\;\;\;(3)\]

Удельная теплоёмкость свинца \(c\) равна 130 Дж/(кг·°C), удельная теплота плавления свинца \(\lambda\) равна 25 кДж/кг.

Приравняем (1) и (3), тогда получим:

\[0,5m\left( {\upsilon _0^2 — {\upsilon ^2}} \right) = cm\left( {{t_п} — {t_0}} \right) + \lambda \Delta m\]

Теперь поделим обе части уравнения на массу пули \(m\):

\[0,5\left( {\upsilon _0^2 — {\upsilon ^2}} \right) = c\left( {{t_п} — {t_0}} \right) + \lambda \frac{{\Delta m}}{m}\]

Учитывая, что \(\alpha = \frac{{\Delta m}}{m}\) (смотрите формулу (2)), имеем:

\[0,5\left( {\upsilon _0^2 — {\upsilon ^2}} \right) = c\left( {{t_п} — {t_0}} \right) + \lambda \alpha \]

Осталось только выразить величину \(\alpha\):

\[\alpha = \frac{{0,5\left( {\upsilon _0^2 — {\upsilon ^2}} \right) — c\left( {{t_п} — {t_0}} \right)}}{\lambda }\]

Произведём вычисления:

\[\alpha = \frac{{0,5 \cdot \left( {{{400}^2} — {{200}^2}} \right) — 130 \cdot \left( {327 — 27} \right)}}{{25 \cdot {{10}^3}}} = 0,84\]

Ответ: 0,84.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

5.3.16 При выстреле вертикально вверх свинцовая пуля ударилась о неупругое тело
5.3.18 Свинцовая пуля, летящая горизонтально со скоростью 500 м/с, пробивает
5.3.19 С какой скоростью должна лететь свинцовая пуля, чтобы расплавиться при ударе