Условие задачи:
Свинцовый шарик радиусом 0,5 см помещён в глицерин. Определить заряд шарика, если в однородном электрическом поле шарик оказался взвешенным в глицерине. Электростатическое поле направлено вертикально вверх и его напряженность 4 кВ/см.
Задача №6.2.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(r=0,5\) см, \(E=4\) кВ/см, \(q-?\)
Решение задачи:
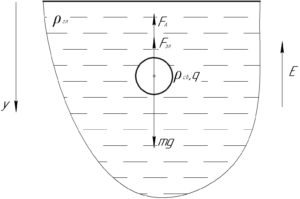 Шарик оказался взвешенным в глицерине (то есть плавающим) под действием трёх сил: силы тяжести \(mg\), силы Архимеда \(F_А\) и электрической силы \(F_{эл}\). Запишем первый закон Ньютона в проекции на ось \(y\):
Шарик оказался взвешенным в глицерине (то есть плавающим) под действием трёх сил: силы тяжести \(mg\), силы Архимеда \(F_А\) и электрической силы \(F_{эл}\). Запишем первый закон Ньютона в проекции на ось \(y\):
\[mg = {F_{эл}} + {F_А}\;\;\;\;(1)\]
Массу свинцового шарика \(m\) определим по формуле (плотность свинца \(\rho_{св}=11300\) кг/м3):
\[m = \rho_{св} V\]
Из математики известно, что объем шара \(m\) можно найти по формуле:
\[V = \frac{4}{3}\pi {r^3}\;\;\;\;(2)\]
Тогда имеем:
\[m = \frac{4}{3}\pi {r^3}\rho_{св} \;\;\;\;(3)\]
Силу \(F_{эл}\) можно определить через величину напряженности поля \(E\) и заряд шарика \(q\):
\[{F_{эл}} = Eq\;\;\;\;(4)\]
Силу Архимеда (выталкивающую силу глицерина) \(F_А\) можно найти по известной формуле (плотность глицерина \(\rho_{гл}=1200\) кг/м3):
\[{F_А} = {\rho _{гл}}gV\]
Учитывая формулу (2), имеем:
\[{F_А} = \frac{4}{3}\pi {r^3}{\rho _{гл}}g\;\;\;\;(5)\]
Подставим выражения (3), (4) и (5) в равенство (1):
\[\frac{4}{3}\pi {r^3}{\rho _{св}}g = Eq + \frac{4}{3}\pi {r^3}{\rho _{гл}}g\]
\[Eq = \frac{4}{3}\pi {r^3}\left( {{\rho _{св}} — {\rho _{гл}}} \right)g\]
В итоге получим такую окончательную формулу:
\[q = \frac{{4\pi {r^3}\left( {{\rho _{св}} — {\rho _{гл}}} \right)g}}{{3E}}\]
Численное значение заряда свинцового шарика \(q\) равно:
\[q = \frac{{4 \cdot 3,14 \cdot {{\left( {0,5 \cdot {{10}^{ — 2}}} \right)}^3} \cdot \left( {11300 — 1200} \right) \cdot 10}}{{3 \cdot 4 \cdot {{10}^5}}} = 0,132 \cdot {10^{ — 6}}\;Кл = 0,132\;мкКл\]
Ответ: 0,132 мкКл.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.39 Между горизонтальными пластинами заряженного конденсатора, напряженность
6.2.41 Капля массой 10^(-10) г, на которой находится заряд, равный 10 зарядам электрона
6.2.42 Капля массой 10^(-13) кг поднимается вертикально вверх с ускорением 2,2 м/с2

 icodepro.ru
icodepro.ru
в последней формуле надо разделить диаметр на 2, так как в формуле используется радиус. Тогда ответ 16,1 нКл.
Во-первых, в условии дан радиус шарика, я с радиусом и работаю, зачем мне диаметр?
Во-вторых, допустим, что мне был бы дан диаметр. Чтобы в последней формуле появился диаметр, то в ней меняем r на d, но ещё делим на 8 (а не на 2, как Вы предлагаете), так как радиус в этой формуле в степени 3.
Почему на 10^5, если там Кило
Потому что там кВ/см, а не кВ/м