Решение: Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо

Условие задачи:

Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо рабочего, тот аккуратно кладет на неё ящик массой 5 кг. Определить выделившуюся при этом теплоту.

Задача №2.10.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(M=100\) кг, \(\upsilon_0=2\) м/с, \(m=5\) кг, \(Q-?\)

Решение задачи:

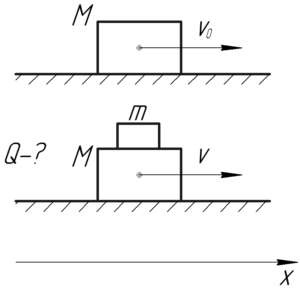Выполним главные действия, необходимые для решения любой задачи на абсолютно неупругий удар — запишем закон сохранения энергии и закон сохранения импульса. Для решения этой задачи этого будет достаточно.

\[\left\{ \begin{gathered}
M{\upsilon _0} = \left( {m + M} \right)\upsilon \;\;\;\;(1)\hfill \\
\frac{{M\upsilon _0^2}}{2} = \frac{{\left( {m + M} \right){\upsilon ^2}}}{2} + Q \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Из равенства (1) выразим скорость тележки после удара:

\[\upsilon = \frac{{M{\upsilon _0}}}{{m + M}}\]

Получившееся выражение подставим в равенство (2).

\[\frac{{M\upsilon _0^2}}{2} = \frac{{\left( {m + M} \right)}}{2}\frac{{{M^2}\upsilon _0^2}}{{{{\left( {m + M} \right)}^2}}} + Q\]

Произведем математические преобразования, чтобы из этого уравнения выразить теплоту \(Q\).

\[Q = \frac{{M\upsilon _0^2}}{2} — \frac{{{M^2}\upsilon _0^2}}{{2\left( {m + M} \right)}}\]

\[Q = \frac{{M\upsilon _0^2}}{2}\left( {1 — \frac{M}{{m + M}}} \right) = \frac{{M\upsilon _0^2}}{2} \cdot \frac{{m + M — M}}{{m + M}}\]

Таким образом, мы получаем решение задачи в общем виде:

\[Q = \frac{{M\upsilon _0^2}}{2} \cdot \frac{m}{{m + M}}\]

Численный ответ будет равен:

\[Q = \frac{{100 \cdot {2^2}}}{2} \cdot \frac{5}{{5 + 100}} = 9,5\; Дж\]