Условие задачи:

Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной плоскости «мертвую петлю» радиусом 3,33 м. Что показывают в верхней точке петли стоящие на тележке пружинные весы, на которых подвешен груз массой 1,2 кг?

Задача №2.4.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(H=10\) м, \(R=3,33\) м, \(m=1,2\) кг, \(F_{упр}-?\)

Решение задачи:

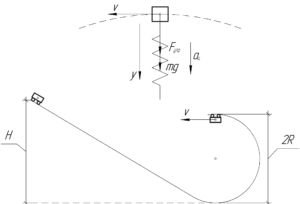Если перефразировать вопрос задачи, то нам нужно найти силу упругости \(F_{упр}\). Рисовать мертвую петлю с тележкой в её верхней точке, конечно же, нет смысла — достаточно нарисовать груз и пружину (пружинные весы). На груз действуют две силы: сила тяжести \(mg\) и сила упругости \(F_{упр}\). При этом груз вместе с тележкой движется с некоторой скоростью \(\upsilon\) по окружности. Значит второй закон Ньютона в проекции на ось \(y\) запишемся так:

\[mg + {F_{упр}} = m{a_ц}\]

Зная скорость груза \(\upsilon\) и радиус петли \(R\), центростремительное ускорение \(a_ц\) найдем по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

\[mg + {F_{упр}} = m\frac{{{\upsilon ^2}}}{R}\]

\[{F_{упр}} = m\left( {\frac{{{\upsilon ^2}}}{R} — g} \right)\;\;\;\;(1)\]

Глядя на последнюю формулу, видно, что нам неизвестна лишь скорость груза в верхней точке. Её можно найти по закону сохранения энергии, поскольку на тележку с грузом не действовало неконсервативных сил (например, сила трения или сила сопротивления воздуха). Изначально у груза была потенциальная энергия \(mgH\), в верхней же точке мертвой петли энергия груза будет состоять из кинетической энергии \(\frac{{m{\upsilon ^2}}}{2}\) и потенциальной \(mg \cdot 2R\).

\[mgH = \frac{{m{\upsilon ^2}}}{2} + mg \cdot 2R\]

\[2gH = {\upsilon ^2} + 4gR\]

\[{\upsilon ^2} = 2g\left( {H — 2R} \right)\]

Подставим последнее выражение в формулу (1), тогда:

\[{F_{упр}} = m\left( {\frac{{2g\left( {H — 2R} \right)}}{R} — g} \right)\]

В скобках приведем под общий знаменатель, предварительно раскрыв скобки в числителе:

\[{F_{упр}} = m\left( {\frac{{2gH — 4gR — gR}}{R}} \right)\]

\[{F_{упр}} = mg\left( {\frac{{2H — 5R}}{R}} \right)\]

Все численные данные даны в системе СИ, поэтому сразу переходим к расчету ответа:

\[{F_{упр}} = 1,2 \cdot 10\left( {\frac{{2 \cdot 10 — 5 \cdot 3,33}}{{3,33}}} \right) = 12,1\; Н\]

Ответ: 12,1 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.33 Спортивный молот — ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное