Условие задачи:
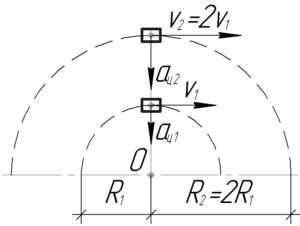
Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз изменится центростремительное ускорение при увеличении скорости в два раза, если радиус окружности также увеличился в два раза?
Задача №1.8.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_2=2\upsilon_1\), \(R_2=2R_1\), \(\frac{a_{ц2}}{a_{ц1}}-?\)
Решение задачи:
 Центростремительное ускорение тела, движущегося по окружности радиуса \(R\) со скоростью \(\upsilon\), можно определить по такой формуле:
Центростремительное ускорение тела, движущегося по окружности радиуса \(R\) со скоростью \(\upsilon\), можно определить по такой формуле:
\[a_ц = \frac{{{\upsilon ^2}}}{R}\]
Найдем отношение ускорений после и до изменения:
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{\upsilon _2^2 \cdot {R_1}}}{{{R_2} \cdot \upsilon _1^2}}\]
Теперь выразим конечную скорость и радиус через начальные, используя то, что дано в условии, т.е. \(\upsilon_2=2\upsilon_1\), \(R_2=2R_1\).
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{4\upsilon _1^2 \cdot {R_1}}}{{2{R_1} \cdot \upsilon _1^2}} = \frac{4}{2} = 2\]
Ответ: увеличится в 2 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.10 Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость
1.8.12 Тело движется равномерно по окружности. Во сколько раз увеличится
1.8.13 Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с-1. Определить

 icodepro.ru
icodepro.ru