Условие задачи:
Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось вращения расположена над полом на высоте 2 м. При прохождении нижнего положения нить обрывается, и тело падает на пол на расстоянии 4 м (по горизонтали) от точки обрыва. Определить силу натяжения нити в момент её обрыва.
Задача №2.4.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=0,1\) кг, \(l=1\) м, \(H=2\) м, \(S=4\) м, \(T-?\)
Решение задачи:
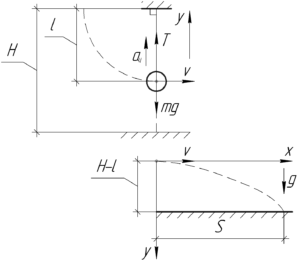 Запишем второй закон Ньютона в проекции на ось \(y\), когда тело будет находиться в нижней точке (смотри верхнюю часть схемы):
Запишем второй закон Ньютона в проекции на ось \(y\), когда тело будет находиться в нижней точке (смотри верхнюю часть схемы):
\[T — mg = ma_ц\]
Радиус кривизны траектории в этой точке равен длине нити \(l\), скорость тела — некоторой \(\upsilon\), тогда центростремительное ускорение \(a_ц\) можно найти по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]
\[T — mg = m\frac{{{\upsilon ^2}}}{l}\]
\[T = m\left( {g + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(1)\]
После обрыва нити тело будет двигать в поле тяжести Земли некоторое время \(t\). Уравнения движения в проекции на ось \(x\) и \(y\) (нижняя часть схемы) дадут такую систему:
\[\left\{ \begin{gathered}
ox:S = \upsilon t \;\;\;\;(2)\hfill \\
oy:H — l = \frac{{g{t^2}}}{2} \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Вообще по формуле (1) видно, что нам нужно найти скорость тела \(\upsilon\), чтобы решить эту задачу. Поэтому из равенства (3) мы выразим время падения \(t\):
\[t = \sqrt {\frac{{2\left( {H — l} \right)}}{g}} \]
Из равенства (2) мы выразим скорость \(\upsilon\):
\[\upsilon = \frac{S}{t}\]
\[\upsilon = S\sqrt {\frac{g}{{2\left( {H — l} \right)}}} \]
Полученное выражение подставим в (1), в итоге:
\[T = m\left( {g + \frac{{g{S^2}}}{{2\left( {H — l} \right)l}}} \right)\]
\[T = mg\left( {1 + \frac{{{S^2}}}{{2\left( {H — l} \right)l}}} \right)\]
Задача решена в общем виде, теперь считаем ответ:
\[T = 0,1 \cdot 10 \cdot \left( {1 + \frac{{{4^2}}}{{2\left( {2 — 1} \right) \cdot 1}}} \right) = 9\; Н\]
Ответ: 9 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение

 icodepro.ru
icodepro.ru
Отличное решение, спасибо. Только вот рисунок немного непривычный, но это на вкус и цвет
Тут можно гораздо легче решить.
T=m(g+a)
T=m(g+(v^2)/R). V=?2gh= ?20•4= ?80
T= 0.1(10+(80/1))
T= 0.1•90
T=9
Это где в условии написано, что H равно 4 м?
Не понимаю логики, по которой Вы нашли скорость \(\upsilon\).
у вас 80 из под корня не выведен так что ваше решение неверна