Решение: Тело массы m движется под действием двух равных по модулю взаимно

Условие задачи:

Тело массы \(m\) движется под действием двух равных по модулю взаимно перпендикулярных сил. Как изменится модуль ускорения тела, если модули этих сил увеличить в 2 раза, а направление одной силы изменить на противоположное?

Задача №2.1.88 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m\), \(F_2=2F_1\), \(\frac{a_2}{a_1}-?\)

Решение задачи:

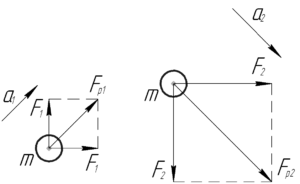На схеме слева представлена начальная ситуация, справа — ситуация после изменения сил. По второму закону Ньютона ускорение тела в первом случае равно:

\[{a_1} = \frac{{{F_{р1}}}}{m}\]

Здесь \(F_{р1}\) — равнодействующая сил, модуль которой можно найти по теореме Пифагора:

\[F_{р1} = \sqrt {F_1^2 + F_1^2} = \sqrt 2 {F_1}\]

Тогда:

\[{a_1} = \frac{{\sqrt 2 {F_1}}}{m}\]

Во втором случае смена направления одной из сил также меняет направление действия равнодействующей и, соответственно, ускорения, но действующие силы также остаются взаимно перпендикулярными. Поэтому аналогично:

\[{a_2} = \frac{{{F_{р2}}}}{m}\]

\[F_{р2} = \sqrt {F_2^2 + F_2^2} = \sqrt 2 {F_2}\]

\[{a_2} = \frac{{\sqrt 2 {F_2}}}{m}\]

Так как \(F_2=2F_1\), то:

\[{a_2} = \frac{{2\sqrt 2 {F_1}}}{m}\]

Ускорение тела изменится на величину следующего соотношения:

\[\frac{{{a_2}}}{{{a_1}}} = \frac{{2\sqrt 2 {F_1} \cdot m}}{{m \cdot \sqrt 2 {F_1}}} = 2\]