Условие задачи:
Тело первую половину пути двигалось со скоростью 12 км/ч. После этого половину времени — со скоростью 7 км/ч, а другую половину времени — со скоростью 5 км/ч. Какова средняя скорость на всем пути?
Задача №1.2.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=\frac{1}{2}S\), \(\upsilon_1=12\) км/ч, \(\upsilon_2=7\) км/ч, \(\upsilon_3=5\) км/ч, \(t_2=t_3\), \(\upsilon_{ср}-?\)
Решение задачи:
Начнем решать задачу с конца, то есть запишем формулу для определения средней скорости:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2} + {S_3}}}{{{t_1} + {t_2} + {t_3}}}\]
Весь путь обозначим буквой \(S\). Так как время \(t_2\) и \(t_3\) равны по условию, то запишем формулу немного проще.
\[{\upsilon _{ср}} = \frac{S}{{{t_1} + 2{t_2}}}\]
Первый отрезок пути \(S_1\) равен половине полного пути \(S\) и проходился телом со скоростью \(\upsilon_1\), поэтому время \(t_1\) определяется по такой простой формуле:
\[{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} = \frac{S}{{2{\upsilon _1}}}\]
Оставшиеся отрезки пути \(S_2\) и \(S_3\) в сумме также дают половину всего пути \(S\).
\[{S_2} + {S_3} = \frac{1}{2}S\]
Справедливо записать эту формулу таким образом:
\[{\upsilon _2}{t_2} + {\upsilon _3}{t_3} = \frac{1}{2}S\]
Так как \(t_2=t_3\), то:
\[{\upsilon _2}{t_2} + {\upsilon _3}{t_2} = \frac{1}{2}S\]
\[{t_2}\left( {{\upsilon _2} + {\upsilon _3}} \right) = \frac{1}{2}S \Rightarrow {t_2} = \frac{S}{{2\left( {{\upsilon _2} + {\upsilon _3}} \right)}} \Rightarrow 2{t_2} = \frac{S}{{{\upsilon _2} + {\upsilon _3}}}\]
Подставим полученные выражения для \(t_1\) и \(2t_2\) в самую первую формулу.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{2{\upsilon _1}}} + \frac{S}{{{\upsilon _2} + {\upsilon _3}}}}} = \frac{S}{{\frac{{S\left( {2{\upsilon _1} + {\upsilon _2} + {\upsilon _3}} \right)}}{{2{\upsilon _1}\left( {{\upsilon _2} + {\upsilon _3}} \right)}}}} = \frac{{S \cdot 2{\upsilon _1}\left( {{\upsilon _2} + {\upsilon _3}} \right)}}{{S\left( {2{\upsilon _1} + {\upsilon _2} + {\upsilon _3}} \right)}} = \frac{{2{\upsilon _1}\left( {{\upsilon _2} + {\upsilon _3}} \right)}}{{2{\upsilon _1} + {\upsilon _2} + {\upsilon _3}}}\]
Остается самое простое действие в этой задаче — подсчитать ответ.
\[{\upsilon _{ср}} = \frac{{2 \cdot 12\left( {7 + 5} \right)}}{{2 \cdot 12 + 7 + 5}} = 8\; км/ч = 2,22\; м/с\]
Ответ: 2,22 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.9 Катер прошел первую половину пути со скоростью в 2 раза большей, чем вторую
1.2.11 Первую половину пути велосипедист проехал со скоростью в 8 раз большей, чем
1.2.12 Мотоциклист за первые 5 минут проехал 3 км, за последующие 8 минут — 9,6 км и

 icodepro.ru
icodepro.ru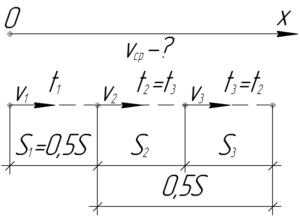
потерян коэффициент 1/2 у второго слагаемого в формуле для средней скорости
Перед тем, когда все начинаете подставлять в формулу
в конце вместе общей скорости написано первая скорость
Откорректировано, спасибо за замечание!
Здраствуйте. У меня вопрос: можно написать решение как: V(ср.)=S/2t(1), так как t(1)=t(2)+t(3), если t(1)=S/2V(1), то V(ср.)=V(1)? Если нет, можете пожалуйста обьяснить. Заранее спасибо, и спасибо за чудесный сайт!
Вы неверно считаете, что \(t_1 = t_2 + t_3\).
Прочтите внимательно условие, там говорится: «Тело первую половину пути (а не времени!) двигалось со скоростью 12 км/ч. После этого половину времени – со скоростью 7 км/ч, а другую половину времени – со скоростью 5 км/ч.»
Помогли, спасибо!!!!