Условие задачи:
Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов уменьшилась сила тяжести, действующая на него?
Задача №2.5.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=1600\) км, \(\frac{\Delta F_т}{F_{т1}}-?\)
Решение задачи:
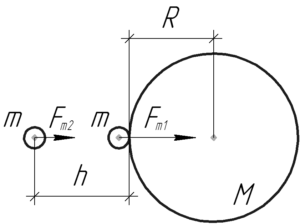 Чтобы ответить на вопрос задачи, нужно найти значение следующего выражения и выразить его в процентах:
Чтобы ответить на вопрос задачи, нужно найти значение следующего выражения и выразить его в процентах:
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{{F_{т1}} — {F_{т2}}}}{{{F_{т1}}}}\;\;\;\;(1)\]
Силу тяжести на поверхности Земли можно определить по такой формуле (это закон всемирного тяготения):
\[{F_{т1}} = G\frac{{Mm}}{{{R^2}}}\;\;\;\;(2)\]
Здесь \(G\) — гравитационная постоянная, \(M\) — масса Земли, \(m\) — масса тела, \(R\) — радиус Земли.
Сила тяжести на высоте \(h\) от поверхности Земли определяется так:
\[{F_{т2}} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}\;\;\;\;(3)\]
Подставляя выражения (2) и (3) в формулу (1), получим:
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{G\frac{{Mm}}{{{R^2}}} — G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}}}{{G\frac{{Mm}}{{{R^2}}}}}\]
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{\frac{1}{{{R^2}}} — \frac{1}{{{{\left( {R + h} \right)}^2}}}}}{{\frac{1}{{{R^2}}}}}\]
Домножим и числитель, и знаменатель на \(R^2\):
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = 1 — \frac{{{R^2}}}{{{{\left( {R + h} \right)}^2}}}\]
Приведем под общий знаменатель и распишем в числителе разность квадратов:
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{{{\left( {R + h} \right)}^2} — {R^2}}}{{{{\left( {R + h} \right)}^2}}}\]
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{h\left( {2R + h} \right)}}{{{{\left( {R + h} \right)}^2}}}\]
Остаётся последнее действие — сосчитать ответ. Напомним, что радиус Земли \(R\) равен 6,4·106 м. Также переведем высоту \(h\) в систему СИ:
\[1600\; км = 1,6 \cdot {10^6}\; м\]
\[\frac{{\Delta {F_{т}}}}{{{F_{т1}}}} = \frac{{1,6 \cdot {{10}^6}\left( {2 \cdot 6,4 \cdot {{10}^6} + 1,6 \cdot {{10}^6}} \right)}}{{{{\left( {6,4 \cdot {{10}^6} + 1,6 \cdot {{10}^6}} \right)}^2}}} = 0,36 = 36\% \]
Ответ: 36%.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте

 icodepro.ru
icodepro.ru