Решение: Тело свободно падает с высоты 5 м. Найти среднюю скорость тела на нижней

Условие задачи:

Тело свободно падает с высоты 5 м. Найти среднюю скорость тела на нижней трети пути.

Задача №1.4.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(H=5\) м, \(S_1=\frac{1}{3}H\), \(\upsilon_{ср}-?\)

Решение задачи:

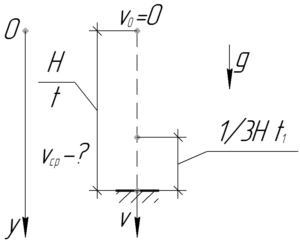Чтобы найти среднюю скорость тела на последней трети пути, нужно этот путь \(\frac{1}{3}H\) разделить на время \(t_1\), которое затратит тело на прохождение этого пути.

\[{\upsilon _{ср}} = \frac{H}{{3{t_1}}}\]

Пусть тело проходит всю высоту \(H\) за \(t\) секунд. Учитывая, что крайнюю треть тело прошло за \(t_1\) секунд, то на предыдущие две трети \(\frac{2}{3}H\) оно должно затратить \(\left( {t — {t_1}} \right)\) секунд. Поскольку движение тела происходит в поле тяжести Земли, причем без начальной скорости, то справедливо записать:

\[\left\{ \begin{gathered}
H = \frac{{g{t^2}}}{2} \hfill \\
\frac{2}{3}H = \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]

Поделим верхнее выражение на нижнее, тогда:

\[{\left( {\frac{t}{{t — {t_1}}}} \right)^2} = \frac{3}{2}\]

Извлечем квадратный корень из обеих частей.

\[\left[ \begin{gathered}
\frac{t}{{t — {t_1}}} = \frac{{\sqrt 3 }}{{\sqrt 2 }} \hfill \\
\frac{t}{{t — {t_1}}} = — \frac{{\sqrt 3 }}{{\sqrt 2 }} \hfill \\
\end{gathered} \right.\]

Нижнее равенство в совокупности отбросим из рассмотрения, поскольку отношение положительных величин заведомо положительное, а в числителе и знаменателе фигурирует время — оно не может быть со знаком «минус».

\[\frac{t}{{t — {t_1}}} = \frac{{\sqrt 3 }}{{\sqrt 2 }}\]

\[\sqrt 2 t = \sqrt 3 t — \sqrt 3 {t_1}\]

\[{t_1} = t\frac{{\sqrt 3 — \sqrt 2 }}{{\sqrt 3 }}\]

Полное время полета \(t\) найдем из первого выражения системы.

\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}} \]

В итоге, время \(t_1\), за которое тело пройдет последнюю треть пути, можно найти по следующей формуле:

\[{t_1} = \frac{{\sqrt 3 — \sqrt 2 }}{{\sqrt 3 }}\sqrt {\frac{{2H}}{g}} \]

С учетом этого, конечная формула для вычисления средней скорости будет выглядеть так:

\[{\upsilon _{ср}} = \frac{{H \cdot \sqrt 3 }}{{3\left( {\sqrt 3 — \sqrt 2 } \right)}}\sqrt {\frac{g}{{2H}}} \]

\[{\upsilon _{ср}} = \frac{{\sqrt {gH} }}{{\sqrt 6 \left( {\sqrt 3 — \sqrt 2 } \right)}}\]

Подставим известные данные, рассчитаем ответ.

\[{\upsilon _{ср}} = \frac{{\sqrt {10 \cdot 5} }}{{\sqrt 6 \left( {\sqrt 3 — \sqrt 2 } \right)}} = 9,08\; м/с = 32,7\; км/ч \]