Решение: Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность

Условие задачи:

Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность, развиваемую тепловозом за это время, если масса тепловоза 600 тонн, а коэффициент трения 0,005.

Задача №2.7.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(t=5\) мин, \(\upsilon=72\) км/ч, \(m=600\) т, \(k=0,005\), \(N_{ср}-?\)

Решение задачи:

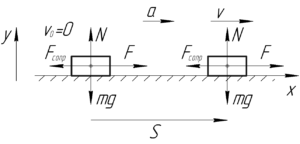Поскольку вектор силы тяги \(\overrightarrow F\) сонаправлен с вектором перемещения \(\overrightarrow S\) (угол между векторами \(\alpha\) равен нулю, т.е. \(\cos \alpha=1\)), то работу этой силы найдем по формуле:

\[A = FS\]

Тогда среднюю мощность \(N_{ср}\), определяемую как отношение совершенной работы ко времени, можно узнать по следующей формуле:

\[{N_{ср}} = \frac{A}{t} = F\frac{S}{t}\;\;\;\;(1)\]

Сначала разберёмся с кинематикой. Если тепловоз движется равноускоренно без начальной скорости и за время \(t\) набирает скорость \(\upsilon\), то ускорение тепловоза найдем из следующих соображений:

\[\upsilon = at\;\;\;\;(2)\]

\[a = \frac{\upsilon }{t}\;\;\;\;(3)\]

При этом он пройдет следующий путь:

\[S = \frac{{a{t^2}}}{2}\]

Принимая во внимание равенство (2), получим:

\[S = \frac{{\upsilon t}}{2}\;\;\;\;(4)\]

Для определения величины силы тяги запишем второй закон Ньютона в проекции на ось \(x\):

\[F — {F_{сопр}} = ma\]

Видно, что \(N=mg\) по первому закону Ньютона в проекции на ось \(y\). Поэтому силу сопротивления \(F_{сопр}\) найдем по формуле:

\[{F_{сопр}} = kN = kmg\]

\[F — kmg = ma\]

\[F = m\left( {a + kg} \right)\]