Решение: Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают

Условие задачи:

Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают изохорически так, что его давление падает в 3 раза. Затем газ расширяют при постоянном давлении. Найти произведённую газом работу, если в конечном состоянии его температура оказалось равной первоначальной.

Задача №5.4.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=1\) кг, \(T_1=300\) К, \(V=const\), \(p_2=\frac{p_1}{3}\), \(p=const\), \(T_3=T_1\), \(A-?\)

Решение задачи:

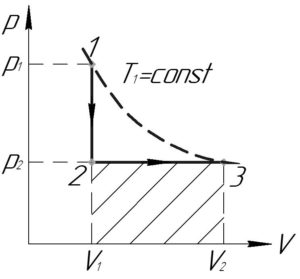Изобразим произведённые над газом процессы в координатах p-V (смотрите схему к решению).

Процесс 1-2 – изохорный (\(V=const\)). Если давление газа в изохорном процессе падает, то по закону Шарля температура газа уменьшается. Работа газа \(A_{12}\) в этом процессе равна нулю, поскольку газ не изменяет своего объема. Площадь фигуры под графиком этого процесса, которая численно равна работе газа, также равна нулю.

Процесс 2-3 – изобарный (\(p=const\)), работу газа \(A_{23}\) в этом процессе можно найти как площадь фигуры под графиком этого процесса (на схеме – заштриховано).

\[{A_{23}} = {p_2}\left( {{V_2} – {V_1}} \right)\]

Искомая суммарная работа газа \(A\) равна сумме работ газа в процессах 1-2 и 2-3:

\[A = {A_{12}} + {A_{23}}\]

Так как \(A_{12}=0\), то имеем:

\[A = {p_2}\left( {{V_2} – {V_1}} \right) = {p_2}{V_2} – {p_2}{V_1}\;\;\;\;(1)\]

В условии сказано, что конечная температура газа \(T_3\) равна начальной \(T_1\), то есть эти точки лежат на одной изотерме (разумеется условной). Запишем закон Бойля-Мариотта для точек 1 и 3:

\[{p_2}{V_2} = {p_1}{V_1}\;\;\;\;(2)\]

Учитывая, что давление газа \(p_2\) в 3 раза меньше давления \(p_1\) (\(p_2=\frac{p_1}{3}\)), и равенство (2), формула (1) примет вид:

\[A = {A_{23}} = {p_1}{V_1} – \frac{1}{3}{p_1}{V_1} = \frac{2}{3}{p_1}{V_1}\]

Запишем уравнение Клапейрона-Менделеева для состояния газа в точке 1:

\[{p_1}{V_1} = \frac{m}{M}R{T_1}\]

Молярная масса водорода (химическая формула H₂) равна 2 г/моль (в СИ – 0,002 кг/моль).

Тогда решение задачи получится таким:

\[A = \frac{2}{3}\frac{m}{M}R{T_1}\]

Подставим значения величин в эту формулу и посчитаем численный ответ задачи:

\[A = \frac{2}{3} \cdot \frac{1}{{0,002}} \cdot 8,31 \cdot 300 = 831000\;Дж = 831\;кДж\]