Решение: Найти работу газа, совершенную в процессе 1-2-3

Условие задачи:

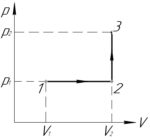\(V_1=2\) л, \(V_2=3\) л, \(p_1=400\) кПа, \(p_2=600\) кПа. Найти работу газа, совершенную в процессе 1-2-3 (схема к задаче приведена справа).

Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_1=2\) л, \(V_2=3\) л, \(p_1=400\) кПа, \(p_2=600\) кПа, \(A-?\)

Решение задачи:

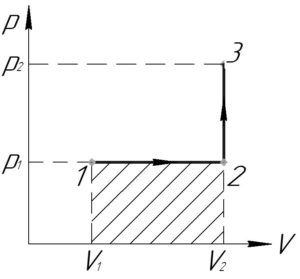Работа газа \(A\), совершенная в процессе 1-2-3, равна сумме работ газа в процессах 1-2 и 2-3.

\[A = {A_{1 – 2}} + {A_{2 – 3}}\;\;\;\;(1)\]

Процесс 1-2 – изобарный, поэтому работу газа \(A_{1 – 2}\) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению – заштриховано):

\[{A_{1 – 2}} = {p_1}\left( {{V_2} – {V_1}} \right)\]

Процесс 2-3 – изохорный, работа газа \(A_{2 – 3}\) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).

\[{A_{2 – 3}} = 0\]

В итоге формула (1) примет такой вид:

\[A = {p_1}\left( {{V_2} – {V_1}} \right)\]

Переведём объемы газа \(V_1\) и \(V_2\) в систему СИ:

\[2\;л = 2 \cdot {10^{ – 3}}\;м^3\]

\[3\;л = 3 \cdot {10^{ – 3}}\;м^3\]

Посчитаем ответ:

\[A = 400 \cdot {10^3} \cdot \left( {3 \cdot {{10}^{ – 3}} – 2 \cdot {{10}^{ – 3}}} \right) = 400\;Дж\]