Решение: При выстреле вертикально вверх свинцовая пуля ударилась о неупругое тело

Условие задачи:

При выстреле вертикально вверх свинцовая пуля ударилась о неупругое тело и расплавилась. На какой высоте произошло это столкновение, если начальная скорость пули 510 м/с, а температура 27 °C. 50% выделившейся теплоты пошло на нагревание.

Задача №5.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=510\) м/с, \(t_0=27^\circ\) C, \(\alpha=50\%\), \(h-?\)

Решение задачи:

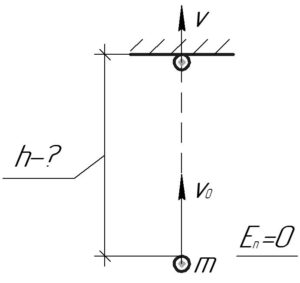Выберем нуль потенциальной энергии на уровне начального положения пули.

Начальная кинетическая энергия пули \(E_{к0}\) перейдёт на высоте \(h\) (то есть перед ударом) в потенциальную энергию \(E_{п}\) и кинетическую энергию \(E_{к}\). В момент удара о неупругое тело кинетическая энергия \(E_{к}\) перейдёт в теплоту \(Q\), часть которой увеличивает внутреннюю энергию пули (из-за этого она и плавится). Запишем закон сохранения энергии для двух описанных случаев:

\[\left\{ \begin{gathered}
{E_{к0}} = {E_п} + {E_к} \hfill \\
{E_к} = Q \hfill \\
\end{gathered} \right.\]

Очевидно, что два этих уравнения можно записать в виде одного:

\[{E_{к0}} = {E_п} + Q\;\;\;\;(1)\]

Обратите внимание, что \(Q\) – это полное выделившееся количество теплоты. По условию лишь 50% (\(\alpha\) часть) выделившейся теплоты пошло на нагревание пули, поэтому справедливо:

\[{Q_1} = \alpha Q\;\;\;\;(2)\]

С другой стороны, чтобы расплавить пулю, её необходимо сначала нагреть до температуры плавления (\(t_п=327^\circ\) C). Поэтому количество теплоты \(Q_1\) также можно выразить следующим способом:

\[{Q_1} = cm\left( {{t_п} – {t_0}} \right) + \lambda m\;\;\;\;(3)\]

Здесь \(c\) – удельная теплоёмкость свинца, равная 130 Дж/(кг·°C), \(\lambda\) – удельная теплота плавления свинца, равная 25 кДж/кг.

Приравняем (2) и (3) и выразим \(Q\):

\[\alpha Q = cm\left( {{t_п} – {t_0}} \right) + \lambda m\]

\[Q = \frac{m}{\alpha }\left( {c\left( {{t_п} – {t_0}} \right) + \lambda } \right)\]

Получившееся выражение для количества теплоты \(Q\) подставим в (1), также в равенстве (1) распишем начальную кинетическую энергию пули \(E_{к0}\) и потенциальную энергию \(E_{п}\) по известным формулам, тогда получим:

\[\frac{{m\upsilon _0^2}}{2} = mgh + \frac{m}{\alpha }\left( {c\left( {{t_п} – {t_0}} \right) + \lambda } \right)\]

Обе части сократим на массу пули \(m\):

\[0,5\upsilon _0^2 = gh + \frac{1}{\alpha }\left( {c\left( {{t_п} – {t_0}} \right) + \lambda } \right)\]

Осталось только выразить высоту \(h\):

\[h = \frac{1}{g}\left( {0,5\upsilon _0^2 – \frac{1}{\alpha }\left( {c\left( {{t_п} – {t_0}} \right) + \lambda } \right)} \right)\]

Посчитаем ответ, подставив значения всех величин в последнюю формулу (величины, данные в процентах, следует подставлять в долях единицы):

\[h = \frac{1}{{10}}\left( {0,5 \cdot {{510}^2} – \frac{1}{{0,5}}\left( {130 \cdot \left( {327 – 27} \right) + 25 \cdot {{10}^3}} \right)} \right) = 205\;м\]