Решение: Свинцовая пуля, летящая горизонтально со скоростью 500 м/с, пробивает

Условие задачи:

Свинцовая пуля, летящая горизонтально со скоростью 500 м/с, пробивает вертикальную доску на высоте 2 м над землей и нагревается на 200 К. На каком расстоянии от доски пуля упала на землю, если всё выделившееся тепло пошло на нагревание пули?

Задача №5.3.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=500\) м/с, \(h=2\) м, \(\Delta T=200\) К, \(S-?\)

Решение задачи:

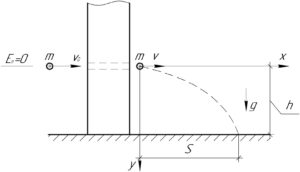Рассмотрим движение пули после пробивания доски. Пусть \(\upsilon\) – скорость пули после прохождения сквозь доску. Запишем уравнения движения пули в проекциях на ось \(x\) и \(y\) (по сути это движение тела, брошенного горизонтально, в поле силы тяжести):

\[\left\{ \begin{gathered}
S = \upsilon t \;\;\;\;(1)\hfill \\
h = \frac{{g{t^2}}}{2} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Из формулы (2) выразим время движения \(t\):

\[t = \sqrt {\frac{{2h}}{g}} \]

Полученное выражение для времени \(t\) подставим в формулу (1):

\[S = \upsilon \sqrt {\frac{{2h}}{g}} \;\;\;\;(3)\]

Отлично, чтобы решить задачу, нам необходимо найти скорость пули \(\upsilon\). Примем нуль потенциальной энергии на уровне положения пули перед входом в доску. Запишем закон сохранения энергии (ЗСЭ) для момента до и после прохождения пулей доски:

\[{E_{к0}} = {E_к} + Q\]

Здесь \(E_{к0}\) – начальная кинетическая энергия пули, \(E_{к}\) – кинетическая энергия пули после пробивания доски, \(Q\) – количество теплоты, которое выделилось при прохождении доски и пошло на нагревание пули. Распишем все перечисленные величины, тогда:

\[\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + cm\Delta T\]

Скажем сразу, что удельная теплоёмкость свинца \(с\) равна 130 Дж/(кг·К).

Сократим в обеих частях равенства на массу \(m\) и домножим на 2, тогда:

\[\upsilon _0^2 = {\upsilon ^2} + 2c\Delta T\]

Выразим скорость \(\upsilon\):

\[\upsilon = \sqrt {\upsilon _0^2 – 2c\Delta T} \]

Полученное выражение подставим в формулу (3), так мы получим решение задачи в общем виде:

\[S = \sqrt {\frac{{2h}}{g}\left( {\upsilon _0^2 – 2c\Delta T} \right)} \]

Посчитаем ответ:

\[S = \sqrt {\frac{{2 \cdot 2}}{{10}}\left( {{{500}^2} – 2 \cdot 130 \cdot 200} \right)} = 281,4\;м\]